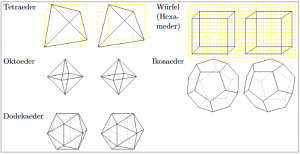
Platonische Körper
Die Platonischen Körper (oder: ideale Körper, reguläre Polyeder — „Vielflächner“) sind konvexe Körper mit einer größtmöglichen Regelmäßigkeit, die nach dem griechischen Philosophen Platon (427–347 v. Chr.) benannt wurden. (Dabei heißt ein Körper konvex, wenn mit je zwei seiner Punkte ![]() und
und ![]() auch alle Punkte auf der Verbindungsstrecke
auch alle Punkte auf der Verbindungsstrecke ![]() zu ihm gehören.)
zu ihm gehören.)
Diese („größtmögliche“) Regelmäßigkeit besteht darin, dass bei jedem dieser Körper alle Seitenflächen zueinander kongruent („deckungsgleich“) sind und dass diese in jeder Ecke in gleicher Weise zusammentreffen.
Es gibt genau fünf Platonische Körper: