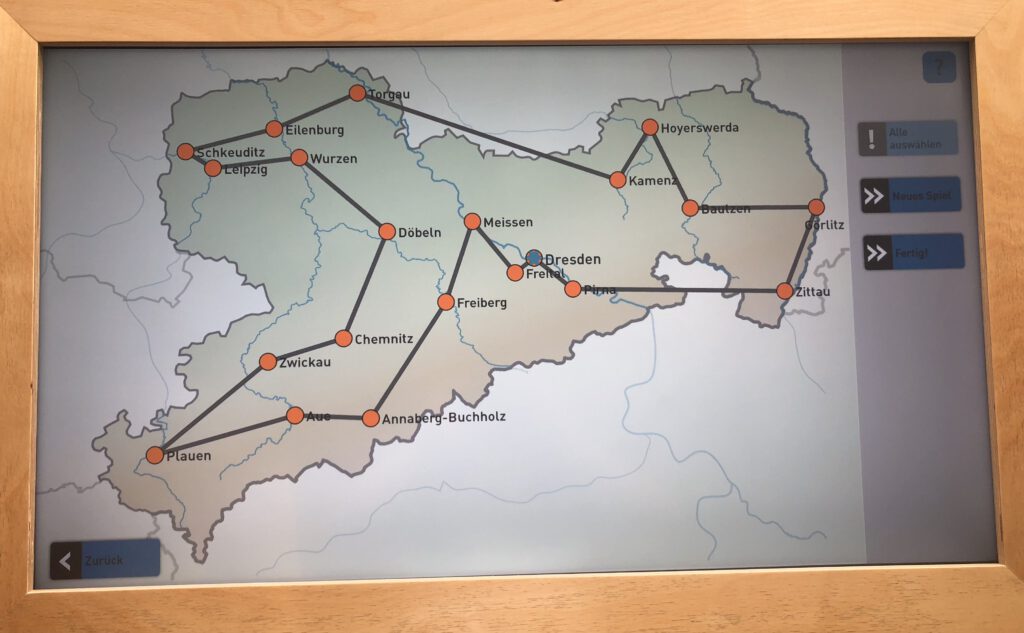
Rundreise durch Sachsen
Stell dir vor, du planst eine Rundreise durch die größten Städte Sachsens. Dabei willst du jede Stadt nur einmal besuchen und es soll ein möglichst kurzer Rundweg zurücklegt werden. Das Exponat „Rundreise durch Sachsen“ ermöglicht dir dabei, deine Reise so effizient wie möglich zu planen.