Satz des Pythagoras

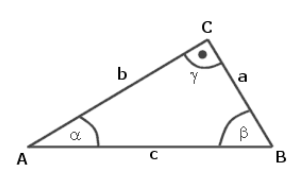
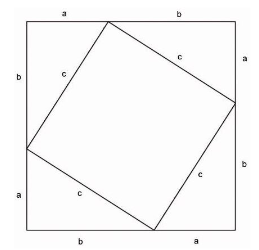
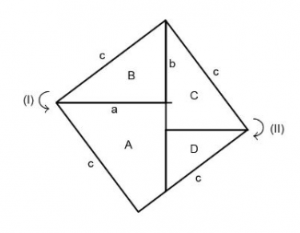
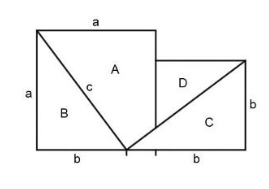
Der Satz des Pythagoras ist einer der fundamentalen Sätze der zweidimensionalen Geometrie. Er besagt, dass bei allen rechtwinkligen Dreiecken (vgl. Abbildung 1) die Seitenlängen in einem bestimmten Verhältnis zueinander stehen: Bildet man über den drei Seiten jeweils ein Quadrat, so ist die Summe der Flächen der beiden kleineren Quadrate (über den Katheten $a$ und $b$ ) genau so groß wie die Fläche des großen Quadrats (über der Hypotenuse $c$ ). Als Gleichung ausgedrückt lautet der Satz des Pythagoras also schlicht $a^2+b^2=c^2$ .

Pythagoras selbst wurde um 570 v. Chr. auf der griechischen Insel Samos als Sohn eines Goldschmiedes geboren. Nachdem er sich durch Studien bei gelehrten Priestern und auf Reisen mit dem damaligen Wissen, vor allem der babylonischen und der ägyptischen Wissenschaft, vertraut gemacht hatte, gründete Pythagoras eine eigene Schule, mit der er seine Schüler zur „inneren Reinheit“ führen wollte. Pythagoras verordnete seinen Schülern mathematica und ließ sie sich auf Arithmetik, Geometrie und Musikwissenschaften konzentrieren.

Das Wissen um die Seitenverhältnisse an einem rechtwinkligen Dreieck war schon um 1800 v. Chr. babylonischen Gelehrten und spätestens im 6. Jahrhundert v. Chr. auch in Indien bekannt. Die Rolle, die Pythagoras für die Vermittlung des später nach ihm benannten Satzes und für seinen mathematischen Beweis gespielt hat, ist nicht unumstritten (siehe Abbildung 2).

Und nun … die Mathematik dazu:

Man kennt heute eine Vielzahl von Beweisen für den Satz des Pythagoras. Einer von diesen beruht auf folgender Überlegung (siehe Abbildungen 3a und 3b):

Das äußere Quadrat in Abbildung 3a hat die Seitenlängen $a+b$ und somit die Fläche $A=(a+b)^2$ . Diese Fläche ergibt sich aber auch durch Addition der Flächen $A_1=4\cdot\frac{ab}{2}$ der vier rechtwinkligen Dreiecke mit den Kathetenlänge $a$ und $b$ und der Fläche $A_2=c^2$ des dem großen Quadrat einbeschriebenen verdrehten Quadrates der Seitenlänge $c$ (vgl. Abbildung 3b). Also ist nun

$A=(a+b)^2=a^2+2ab+b^2=4A_1+A_2=2ab+c^2,$

woraus die gewünschte Identität $a^2+b^2=c^2$ durch Subtraktion von $2ab$ auf beiden Seiten folgt.

Das Exponat im ERLEBNISLAND MATHEMATIK zeigt die Richtigkeit des Satzes des Pythagoras auf (eine andere) elementare Weise (siehe die nachfolgenden Abbildungen 4a und 4b):

Durch Umklappen der Fläche $B$ (nach links) und der Fläche $C$ (nach rechts) um die Drehpunkte $(I)$ bzw. $(II)$ bis zum Anschlag (vgl. Abbildung 4a) erhält man aus einem Quadrat mit der Seitenlänge $c$ (also dem Flächeninhalt $c^2$ ) zwei nebeneinander liegende Quadrate mit den Flächeninhalten $a^2$ und $b^2$ (vgl. Abbildung 4b).

Zuletzt noch etwas Literarisches

Wir schließen mit einer — mathematisch nicht ganz ernst zu nehmenden — literarischen Verarbeitung. Der deutsche Dichter Adalbert von Chamisso (1781–1838) schildert das legendäre Opfer, das Pythagoras den Göttern dargebracht haben soll, nachdem er „seinen“ Satz entdeckt hatte:

Vom pythagoreischen Lehrsatz

Die Wahrheit, sie besteht in Ewigkeit,

Wenn erst die blöde Welt ihr Licht erkannt;

Der Lehrsatz nach Pythagoras benannt

Gilt heute, wie er galt zu seiner Zeit.

Ein Opfer hat Pythagoras geweiht

Den Göttern, die den Lichtstrahl ihm gesandt;

Es taten kund, geschlachtet und verbrannt,

Einhundert Ochsen seine Dankbarkeit.

Die Ochsen seit dem Tage, wenn sie wittern,

Daß eine neue Wahrheit sich enthülle,

Erheben ein unmenschliches Gebrülle;

Pythagoras erfüllt sie mit Entsetzen;

Und machtlos sich dem Licht zu widersetzen

Verschließen sie die Augen und erzittern.

(zitiert nach Projekt Gutenberg, Alle Gedichte Adelbert von Chamissos)

Literatur

[1] Dewdney, A.K.: Reise in das Innere der Mathematik, Berlin, 2000.

[2] Fraedrich, A.M.: Die Satzgruppen des Pythagoras, Mannheim, 1995.

[3] Maor, E.: The Pythagorean Theorem: A 4,000-year History, Princeton, 2007.

[4] Schupp, H.: Elementargeometrie, Stuttgart, 1977.

[5] Singh, S.: Fermats letzter Satz, München, 2000.

[6] v. Wedemeyer, I.: Pythagoras, Weisheitslehrer des Abendlandes, Ahlerstedt, 1988.