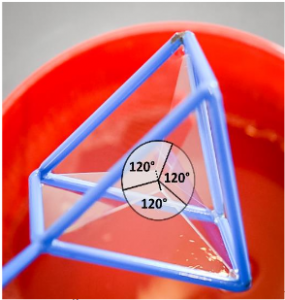
Wunderbare Seifenhäute
Ob man wohl auch „eckige Seifenblasen“ erzeugen kann? Sicher doch! Durch das Tauchen verschiedener Kantenmodelle in Seifenlauge werden die unterschiedlichsten, faszinierenden Gebilde erzeugt. So erweist es sich sogar als recht schwierig, die Oberfläche eines Würfels mit Seifenhaut zu benetzen. Häufiger wird ein viel filigraner wirkendes Gebilde mit einem kleinen Quadrat oder auch Würfel in der Mitte, zu dem sich Seifenhäute von den Würfelkanten spannen, erzeugt: