Parkettierungen

Stell dir vor, du betrittst einen Raum und siehst einen schönen Holzfußboden, der aus gleichmäßig verlegten Holzplatten besteht. Jede dieser Holzplatten besitzt eine rechteckige oder quadratische Form. Außerdem sind sie so angeordnet, dass der gesamte Boden lückenlos und ohne Überlappung bedeckt ist. Diese Art der Anordnung wird als Parkettierung bezeichnet. Das Prinzip findet man nicht nur bei Bodenbelägen, sondern z. B. bei Fliesenmustern und Mosaiken. Auch bei unseren Exponaten „Wer findet den Fisch“, „Penrose-Puzzle“ und „Kängurupuzzle“ kann man eine Parkettierung erkennen. Die Muster unterscheiden sich zwar meist sehr, doch das Grundkonzept bleibt gleich.

Schon im antiken Griechenland wurde das Prinzip der Parkettierung verwendet, insbesondere in der Architektur und bei der Gestaltung von Mosaiken. Die alten Griechen und Römer sind bekannt für ihre komplexen Mosaikarbeiten, bei denen geometrische Muster aus kleinen Stein- oder Glasstücken auf Böden und Wänden angebracht wurden. Heutzutage ist das Prinzip der Parkettierung in der Architektur, Kunst und in der Computertechnik weit verbreitet. Besonders bekannt sind die Werke von M. C. Escher.

Die systematische Untersuchung von Parkettierungen in der modernen Mathematik begann jedoch erst im 19. Jahrhundert. Einer der ersten Forscher, der sich mit Parkettierungen beschäftigte, war der deutsche Mathematiker August Ferdinand Möbius im 19. Jahrhundert. Er konnte mit seinen Erkenntnissen in der Topologie einen fundamentalen Beitrag zur Entstehung der Theorie leisten. Auch der Mathematiker Heinrich Hesch entwickelte umfangreiche Kataloge von Parkettierungen im 20. Jahrhundert. Im folgenden Abschnitt werden wir die mathematische Sichtweise auf Parkettierungen kennenlernen und sehen, welche Arten von Parkettierungen es gibt.

Und nun … die Mathematik

In der Mathematik versteht man unter einer Parkettierung die lückenlose und überlappungsfreie Überdeckung der euklidischen Ebene durch eine oder mehrere geometrische Formen, die sogenannten \emph{Kacheln}. Meist fordert man weitere Regel, wie z. B. dass nur eine Kachelsorte verwendet werden soll. Die Definition einer Parkettierung der Ebene kann auch auf höhere Dimensionen verallgemeinert werden. Wir wollen uns im Folgenden aber auf den Fall der Ebene beschränken. Es gibt viele Arten von Parkettierungen, die sich durch die verwendeten Formen und geforderten Regeln unterscheiden. Wir wollen einige davon untersuchen.

Einfache Parkette

Einfache Parkette sind Parkettierungen, die nur aus einer Sorte von Kacheln bestehen. Man nennt diese Kachel auch \emph{Protokachel}. Oftmals sind Protokacheln symmetrisch. Es gibt aber auch unsymmetrische Protokacheln. So ist unser Känguru Puzzle ein einfaches symmetrisches Parket mit einer Protokachel in Form eines Kängurus (siehe Abbildung 1). Bei unserem Exponat „Beweis ohne Worte: Rautenparkett“ (siehe Abbildung 2) kannst du ein regelmäßiges Sechseck vollständig mit gleich großen Rauten überdecken. Dabei fällt auf: Es gibt genau drei mögliche Ausrichtungen für die Rauten – sie können waagerecht liegen oder schräg nach links oder rechts oben zeigen. Und ganz gleich, wie du die Rauten anordnest: Damit das Sechseck lückenlos gefüllt wird, müssen alle drei Orientierungen gleichermaßen vorkommen. Ein verblüffender Effekt, und ein Beweis ganz ohne Worte!

Euklidische Parkettierungen

Parkettierungen mit konvexen regelmäßigen Polygonen nennt man auch Euklidische Parkettierung. Diese lassen sich in mehrere Arten unterscheiden.

• Reguläre/Platonische Parkettierungen sind einfache Parkettierungen mit einem regelmäßigen Polygon als Protokachel. Es darf dabei nirgends eine Ecke eines Polygons auf eine Seite eines anderen Polygons treffen (Kante-an-Kante Regel). Es gibt genau 3 Reguläre Parkettierungen, die du in Abbildung 3 sehen kannst.

• Archimedische Parkettierungen sind Parkettierungen, die sich aus zwei oder mehr regelmäßigen Polygonen zusammensetzten. Dabei soll die Kante-an-Kante Regel erfüllt sein, alle Seiten gleich lang sein und an jeder Ecke befindet sich dieselbe Anordnung von Polygonen. Es gibt dafür genau 8 verschiedene Möglichkeiten, die du in Abbildung 5 erkennen kannst.

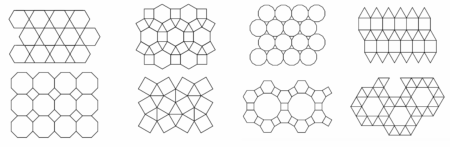
• Semireguläre Parkettierungen bestehen aus zwei oder mehr regelmäßigen Polygonen, sodass die Kante-an-Kante Regel erfüllt ist und an jeder Ecke eine von zwei möglichen Anordnungen von Polygonen auftritt. Es gibt insgesamt 20 verschiedene Semireguläre Parkettierungen.

• Pythagoreische Parkettierungen enthalten zwei unterschiedlich große Quadraten. Jedes Quadrat ist dabei von 4 anderen Quadraten umrandet. Wir bemerken, dass hier die Kante-an-Kante Regel nicht erfüllt sein kann. Ein Beispiel kannst du in Abbildung 6 erkennen.

Aperiodische Parkettierungen

Die eben genannten Arten von Parkettierungen haben eine Eigenschaft gemeinsam. Sie sind nämlich alle Symmetrisch. Anschaulich gesprochen heißt das, dass die Parkettierung ein sich wiederholendes Grundmuster besitzt. Wir können die Parkettierung also so verschieben, das wir wieder das ursprüngliche Muster erhalten. Probiere doch mal im Epsilon aus, in welche Richtung du das Känguru Puzzle schieben musst, damit du wieder dein Ausgangsmuster erhältst. Im Jahre 1973 wurde von Roger Penrose und Robert Amann eine Parkettierung entdeckt, die nicht symmetrisch ist. Die sogenannte Penrose Parkettierung setzt sich dabei aus zwei oder mehreren Kacheln zusammen, wobei die Parkettierung kein sich wiederholendes Muster enthält. Unsere Exponate „Wer findet den Fisch“ oder „Penrose Puzzle“ bilden genau eine solche Penrose Parkettierungen, wie du in Abbildung 7 und Abbildung 8 erkennen kannst.

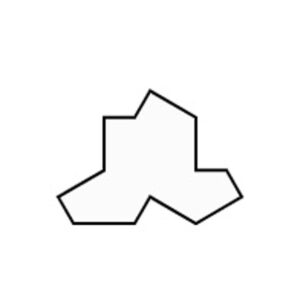
Es gibt übrigens unendlich viele verschiedene aperiodische Parkettierungen. Erst kürzlich konnte aber die Frage beantwortet werden, ob eine aperiodische einfache Parkettierung existiert, d.h. eine mit nur einer Kachelsorte, eine sogenannte Einstein Kachel. Hierbei erfolgte die Namensgebung nicht in Anlehnung an der Physiker Albert Einstein, sondern bezieht sich darauf, dass es sich um genau einen Stein handelt. Im November 2022 fand der bereits pensionierte Druckanlagentechniker David Smith aus Yorkshire nämlich eine solche Kachel. Durch eine Weiterentwicklung seiner Idee konnte sogar gezeigt werden, dass unendlich viele verschiedene Einstein Kacheln existieren. Die ursprüngliche Kachel, den sogenannten „Hat“, kannst du in Abbildung 9 sehen.

Quellen

• Abbildung 3 und 4: https://mathworld.wolfram.com/Tessellation.html
• Abbildung 5: https://en.wikipedia.org/wiki/Pythagorean_tiling
• Abbildung 6: https://www.spektrum.de/news/hobby-mathematiker-findet-lang-ersehnte-einstein-kachel/2124963