Abakus

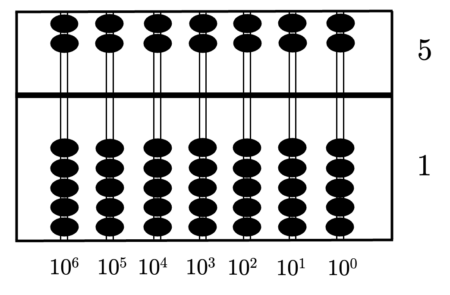
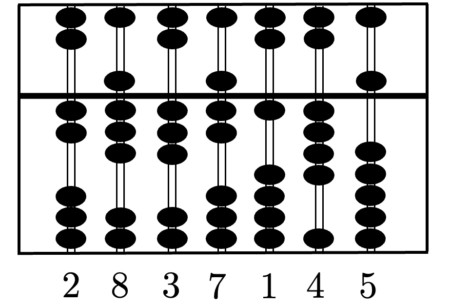
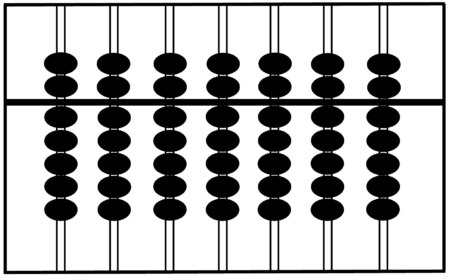
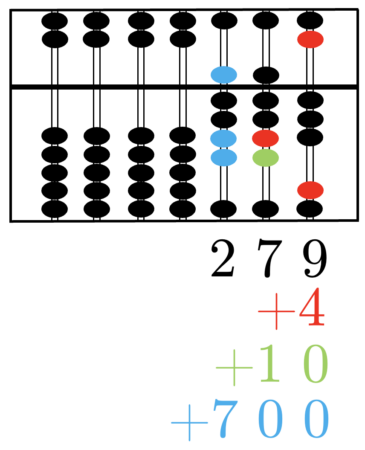
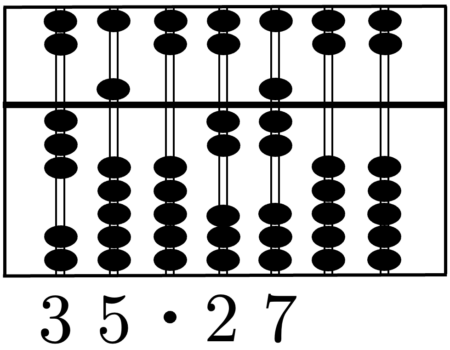
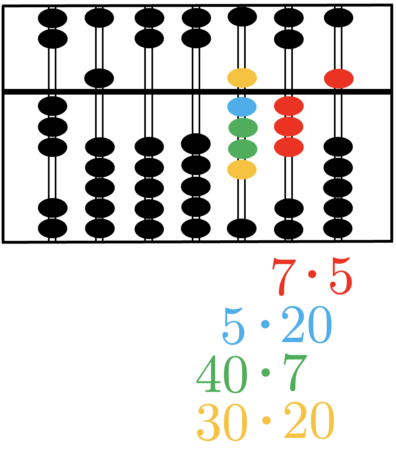
Das Rechnen mit Zahlen und Größen ist ein wesentlicher Bestandteil unserer Gesellschaft. Unsere technologisierte Welt basiert auf Berechnungen mittels Computern oder Großrechnern. Ohne Sie gäbe es keine Globalisierung und erst recht nicht das Internet. Doch das Rechnen mit elektronischen Geräten steht der Menschheit erst seit einer vergleichsweise kurzen Zeit zur Verfügung. Frühere Zivilisationen nutzten dafür mechanische Apparate, sogenannte \emph{Rechenschieber}, auch \emph{Abakus} genannt, mit denen man einfache Kalkulationen vornehmen kann. Sie geraten bei schwierigeren Rechenaufgaben aber schnell an ihre Grenzen, von der Schnelligkeit ganz zu schweigen. Der früheste heute bekannte Abakus konnte in Sumer gefunden werden. Es wird vermutet, dass er von den Babyloner:innen zwischen 2700 und 2300 Jahre vor Christus entwickelt wurde. Eine frühe Version des Abakus, auf welchem unser Exponat basiert, wurde zwischen 206 v.Chr. und 220 n. Chr. in China entwickelt. Die heute klassische Version des sogenannten \emph{Suanpan} wurde im 12. Jahrhundert entwickelt. Er besteht aus einem rechteckigen Holzrahmen, der durch eine Querstrebe in einen oberen, den „Himmel“, und unteren Bereich, die „Erde“, geteilt werden. Vertikal durch den Holzrahmen verlaufen sieben Stäbe, an denen im oberen Teil zwei und im unteren fünf bewegliche Perlen angebracht sind. Man nennt diese Perlen im oberen Bereich auch „Himmelsperlen“ und die im unteren Bereich „Erd-“ oder „Wasserperlen“. Unser Modell eines Abakus entspricht einer eher traditionelleren Fassung. Zu einer späteren Zeit wurde im japanischen Raum eine modernere Versionen mit insgesamt 6 bzw. 5 Perlen entwickelt, wovon eine im Himmel und 5 bzw. 4 im Erdbereich zu finden sind. Wie kann man aber mit dem Suanpan rechnen? Dies wollen wir im folgenden Abschnitt klären.

Abbildung 1: Das Exponat

Und nun … die Mathematik

Die intuitivste Art mit ganzen Zahlen zu rechnen ist das Zählen mit unseren zehn Fingern. So ist diese Art und Weise zu rechnen die erste, die man im Kindergarten lernt. Auf dieser Methode zu rechnen basiert unser heute alltägliches Zahlensystem, das Dezimalsystem. Die Idee dahinter ist, dass jede beliebige Zahl als Vielfache von Potenzen zur Basis 10 dargestellt werden können. So hat z.B. die Zahl 17 die Darstellung
      \[17 = 1 \cdot 10^1 + 7 \cdot 10^0.\]
Hierbei ist die Reihenfolge der Zahlen entscheidend. Die „7“ ist auf der Einerstelle und die „1“ auf der Zehnerstelle. Um diese Zahl mit der Hand angeben zu können, bräuchte man also zwei ganze Hände und sieben Finger. Auch Nachkommastellen können in dieser Weise geschrieben werden. So besitzt die Zahl 3,25 die Darstellung
      \[3,25 = 3 \cdot 10^0 + 2\cdot 10^{-1} + 5 \cdot 10^{-2}.\]
Wir können jede beliebige Zahl in dieser Form schreiben. Wir sagen dazu auch Stellenwertsystem zur Basis 10. Es sind auch andere Zahlensysteme möglich. Computer rechnen z.B. im Binärsystem, also zur Basis 2 und zur Datenverarbeitung rechnet man häufig zur Basis 16, sprich im Hexadezimalsystem.

Arithmetik auf Suanpan

Auch auf dem Suanpan rechnet man zur Basis 10. Dabei haben die Erdperlen jeweils den Wert 1 und die Himmelsperlen den Wert 5. Des Weiteren steht jede Reihe auf dem Abakus für eine bestimmte Dezimalstelle: die ganz rechts für die Einerstellen, die zweite für die Zehnerstellen, die dritte für die Hunderterstellen und so weiter (siehe Abbildung 2).
Abbildung 2: Die Grundstellung des Suan Pan und die Wertigkeit der Perlen

Bevor du mit dem Suan Pan rechnen kannst, musst du ihn in die Grundstellung bringen. Dafür musst du die Erdperlen jeweils ganz nach unten und die Himmelsperlen nach oben schieben, wie in Abbildung 3 dargestellt. Falls du nun die oberste Erdperle auf dem Einerstab nach oben schiebst, dann stellt diese den Zahl 1 dar. Falls du eine weitere Erdperle auf diesem Stab hinzufügst, dann repräsentieren die beiden Perlen die Zahl 2, und so weiter. Dasselbe Prinzip gilt auch für die Himmelsperlen. Schiebst du eine Himmelsperle auf dem Einerstab nach unten, so zählt diese als 5. Die Werte der Himmelsperlen und der Erdperlen addieren sich dabei jeweils, das heißt, falls eine Himmels- und zwei Erdperlen an der Querstrebe anliegen, dann repräsentieren diese die Zahl 7. Identisch stellen die Perlen auf dem Zehnerstab die Zahlen an der Zehnerstelle, die Perlen auf dem Hunderterstab die Hunderterstelle, und so weiter, dar. In Abbildung 3 siehst du z.B. wie die Zahl 2 837 145 auf dem Suan Pan dargestellt werden kann.

Abbildung 3: Darstellung der Zahl 2 837 145 auf dem Suan Pan

Beachte, dass manche Zahlen mehrere Darstellungen auf dem Suan Pan haben. So kannst du die Zahl 10 darstellen, indem du die beiden Himmelsperlen in der Einerstelle nach unten, oder eine Erdperle auf dem Zehnerstab nach oben schiebst. In den meisten Rechnungen benötigt man aber die zweite Himmelsperle nicht. Falls man z.B. die Zahl 15 darstellen möchte, nutzt man stattdessen dafür eine Erdperle auf dem Zehnerstab und und eine Himmelsperle auf dem Einerstab. Aber was ist wohl die größtmögliche Zahl, die man mit dem Suanpan darstellen kann wenn man alle Perlen nutzen möchte?

Abbildung 4: Die größtmöglich darstellbare Zahl
Da der Suan Pan fünf Erdperlen mit Wertigkeit 1 und zwei Himmelsperlen mit Wertigkeit 5 besitzt, ist auf jeder Zehnerstelle also die Zahl 15 darstellbar, sprich wie in Abbildung ?? zu sehen ist die größtmöglich darstellbare Zahl
      \[15 \cdot 10^6 + 15 \cdot 10^5 + 15 \cdot 10^4 + 15 \cdot 10^3 + 15 \cdot 10^2 + 15 \cdot 10^1 + 15 \cdot 10^0 = 16 \, 666 \, 665.\]
Übrigens ist es auch möglich mit Nachkommastellen zu rechnen. Dafür muss man die Einerstelle entsprechend nach links verschieben.

Addition und Subtraktion

Als Rechenbeispiel addieren wir die Zahlen 279 und 714. Nachdem du den Suanpan in die Grundstellung gebracht hat, bewege die Perlen so, dass der erste Summand auf dem Suanpan dargestellt wird. Für unser Beispiel musst du also vier Erd- und eine Himmelsperle auf dem Einerstab, zwei Erd- und eine Himmelsperle auf dem Zehnerstab und zwei Erdperlen auf dem Hunderterstab zu der Querstrebe bewegen. Danach addierst du Stellenweise, beginnend bei der Einerstelle, den zweiten Summanden. Addiere also zuerst 4 zu 9. Um nun die Summe 13 darzustellen, fügst du eine Perle auf dem Zehnerstab hinzu und stellst auf dem Einerstab drei ein. Weiter geht es mit der Zehnerstelle. Schiebe dafür eine Perle auf dem Zehnerstab nach oben. Schließlich musst du nur noch zwei Erd und eine Himmelsperle auf dem Hunderterstab hinzufügen und schon kannst du das Ergebnis ablesen, nämlich 993.
Abbildung 5: Addition der Zahlen 279 und 714 auf dem Suanpan
Diese Art und Weise zu rechnen entspricht genau dem schriftlichen Addieren, das wir in der Grundschule lernen. Das Subtrahieren funktioniert in ähnlicher Weise. Statt jedoch Perlen hinzuzufügen, ziehst du sie ab, indem  du sie von der Querstrebe weg bewegst. Beachte aber, dass der Suanpan keine negativen Zahlen darstellen kann. Der Subtrahend muss also immer kleiner sein als der Minuend.

Multiplikation

Der Suanpan kann dir auch beim Multiplizieren zweier Zahlen helfen. Als Rechenbeispiel multiplizieren wir die Zahlen 35 und 27. Stelle dafür den Suanpan wie in Abbildung 5 dargestellt ein.
Abbildung 6: Multiplikation der Zahlen 35 und 27

Der Unterschied beim Multiplizieren und Addieren ist, dass wir beide Zahlen linksbündig auf dem Suanpan einstellen und zwischen ihnen einen Stab frei lassen. Dies dient der besseren Übersicht beim Multiplizieren der einzelnen Stellen. Als Einerstab für die Darstellung des Produkts legen wir, wie bei der Addition den Stab ganz rechts fest. Anschließend multiplizieren wir stellenweise und stellen das Produkt, wie bei der Addition, auf dem Suanpan ein. Stelle also für unser Beispiel zuerst das Produkt der Einerstellen, also 35, rechtsbündig auf dem Suanpan ein. Als nächstes multiplizieren wir 5 mit 20. Da der Hunderterstab bereits auf die Zahl 7 eingestellt ist, müssen wir nur eine Himmels- und eine Erdperle von der Querstrebe wegbewegen, um das Ergebnis 100 einzustellen. Füge für die Multiplikation von 30 und 7 nun zwei Erdperlen zu dem Hunderterstab und eine auf dem Zehnerstab hinzu. Schließlich müssen wir noch 20 mit 30 multiplizieren. Füge also auf dem Hunderterstab eine Himmels- und eine Erdperle hinzu. Beachte, dass wir bei der Multiplikation den Tausenderstab nicht benötigt haben. Setze also die am Anfang eingestellte zwei zurück. Nun kannst du das Ergebnis auf dem Suanpan ablesen, nämlich 945.

Abbildung 7: Ergebnis der Multiplikation mit 35 und 27

Im Prinzip kannst du mit dem Suan Pan beliebig große Zahlen multiplizieren. Der Suanpan müsste jedoch entsprechend der Anzahl der zu multiplizierenden Stellen verlängert werden.