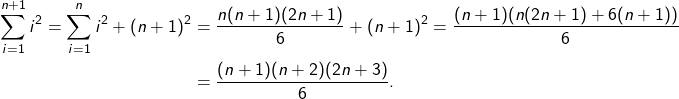Beweis ohne Worte: Summe der Quadratzahlen
Ein „Beweis ohne Worte“ ist so überzeugend, dass man ihn tatsächlich für einen Beweis hält, obwohl er aus der Sicht des Mathematikers keiner ist. Ein solcher eignet sich aber oft sehr gut, um schnell zu einem mathematischen Beweis zu finden. Warum? Die dargestellte Vermutung wird nicht allgemeingültig bewiesen, sondern nur für einige Fälle, z.B. bis ![]() . Ein mathematisch vollständiger Beweis müsste alle möglichen natürlichen Zahlen
. Ein mathematisch vollständiger Beweis müsste alle möglichen natürlichen Zahlen ![]() , also unendlich viele Fälle, abdecken. Das würde man für diese Beispiele hier mit dem Beweisprinzip der vollständigen Induktion machen. Sehr gut geeignet sind die Exponate allerdings, um eine passende Vermutung für eine allgemeine Formel aufzustellen. Dies ist sehr wichtig, denn ohne Vermutung hat man auch nichts, was man beweisen könnte. Außerdem kann man sich nach genauem Beobachten vorstellen, wie der nächste Schritt, dann der übernächste und immer so weiter aussehen würde, was für eine gute Begründung des Sachverhalts ausreicht. Beim Beweis durch vollständige Induktion wird im Prinzip nichts anderes gemacht. Ein solcher Beweis besteht aus zwei Teilen: dem Induktionsanfang und dem Induktionsschritt. Zunächst zeigt man an einem einfachen Fall (meist
, also unendlich viele Fälle, abdecken. Das würde man für diese Beispiele hier mit dem Beweisprinzip der vollständigen Induktion machen. Sehr gut geeignet sind die Exponate allerdings, um eine passende Vermutung für eine allgemeine Formel aufzustellen. Dies ist sehr wichtig, denn ohne Vermutung hat man auch nichts, was man beweisen könnte. Außerdem kann man sich nach genauem Beobachten vorstellen, wie der nächste Schritt, dann der übernächste und immer so weiter aussehen würde, was für eine gute Begründung des Sachverhalts ausreicht. Beim Beweis durch vollständige Induktion wird im Prinzip nichts anderes gemacht. Ein solcher Beweis besteht aus zwei Teilen: dem Induktionsanfang und dem Induktionsschritt. Zunächst zeigt man an einem einfachen Fall (meist ![]() ), dass die aufgestellte Vermutung dafür richtig ist. Dieser erste Schritt wird Induktionsanfang genannt. Dann wird, ausgehend von der Annahme, dass die Vermutung für ein (beliebiges)
), dass die aufgestellte Vermutung dafür richtig ist. Dieser erste Schritt wird Induktionsanfang genannt. Dann wird, ausgehend von der Annahme, dass die Vermutung für ein (beliebiges) ![]() richtig ist, gezeigt, dass die Vermutung dann auch für den Nachfolger
richtig ist, gezeigt, dass die Vermutung dann auch für den Nachfolger ![]() gilt. Veranschaulicht wird das oft durch das Bild einer Leiter, auf der man schon bis zur
gilt. Veranschaulicht wird das oft durch das Bild einer Leiter, auf der man schon bis zur ![]() -ten Stufe geklettert ist, und von dort immer auf die nächste,
-ten Stufe geklettert ist, und von dort immer auf die nächste, ![]() -te Stufe kommt. Wie die Menge der natürlichen Zahlen ist auch diese Leiter als unendlich gedacht. Das Exponat zu der Summe der ungeraden Zahlen besteht aus
-te Stufe kommt. Wie die Menge der natürlichen Zahlen ist auch diese Leiter als unendlich gedacht. Das Exponat zu der Summe der ungeraden Zahlen besteht aus ![]() -förmigen Plastikteilen unterschiedlicher Größen. Das erste Teil besteht aus einem Kästchen, das zweite aus 3, das dritte aus 5, usw., das
-förmigen Plastikteilen unterschiedlicher Größen. Das erste Teil besteht aus einem Kästchen, das zweite aus 3, das dritte aus 5, usw., das ![]() -te Teil aus
-te Teil aus ![]() Kästchen. Wenn man die Anzahl all dieser Kästchen addiert, erhält man also die Summe der ersten
Kästchen. Wenn man die Anzahl all dieser Kästchen addiert, erhält man also die Summe der ersten ![]() ungeraden Zahlen. Das Exponat ermöglicht sogar, dass der Betrachter nicht selber rechnen, sondern nur zusammenlegen muss. Denn die
ungeraden Zahlen. Das Exponat ermöglicht sogar, dass der Betrachter nicht selber rechnen, sondern nur zusammenlegen muss. Denn die ![]() -förmigen Teile passen zusammen und ergeben, in der richtigen Reihenfolge (man darf keine Lücken lassen), jeweils ein Quadrat. Für jedes hinzugenommene Teil (entspricht einem weiteren Summanden beim Addieren) wächst das Quadrat um eine Kästchenlänge in jede Richtung. Genauer gesagt: Wenn man das Teil der Größe
-förmigen Teile passen zusammen und ergeben, in der richtigen Reihenfolge (man darf keine Lücken lassen), jeweils ein Quadrat. Für jedes hinzugenommene Teil (entspricht einem weiteren Summanden beim Addieren) wächst das Quadrat um eine Kästchenlänge in jede Richtung. Genauer gesagt: Wenn man das Teil der Größe ![]() hinzunimmt, dann erhält man ein zusammengelegtes Quadrat mit Kantenlänge
hinzunimmt, dann erhält man ein zusammengelegtes Quadrat mit Kantenlänge ![]() , also
, also ![]() Kästchen groß. Damit kommt man zu der Formel
Kästchen groß. Damit kommt man zu der Formel
![Rendered by QuickLaTeX.com \[1+3+5+\cdots+2n-1=\sum_{i=1}^n{(2n-1)}=n^2.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-4d9ef28d737b271f176c5ab0070b95a0_l3.png)

![Rendered by QuickLaTeX.com \[1+3+5+\cdots+(2n-1)=\sum_{i=1}^n{(2i-1)}=n^2.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-c912fa49ccc26c675194e43feeb1e4f6_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n+1}{(2i-1)}=\sum_{i=1}^n{(2i-1)}+(2(n+1)-1)=n^2+2(n+1)-1=n^2+2n+1=(n+1)^2.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-9c8aaa7918edf741de978958af37ce24_l3.png)
![Rendered by QuickLaTeX.com \[1+2+3+\cdots+n=\sum_{i=1}^n{i}=\frac{n(n+1)}{2}.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-20c1077035c631207e60b317c5886471_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^n{i}=\frac{n(n+1)}{2}\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-ff3f0d39b2f16504ba30fc7879e1e4c1_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n+1}{i}=\frac{(n+1)(n+2)}{2}\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-dbd8e253d96e6ce3eea7724d5aa491b4_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n+1}{i}=\sum_{i=1}^n{i}+(n+1)=\frac{n(n+1)}{2}+n+1=\frac{n(n+1)+2(n+1)}{2}=\frac{(n+2)(n+1)}{2}.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-67a5130e7fb699ae38e7121a773ec9e7_l3.png)

 Quadratzahlen
Quadratzahlen![Rendered by QuickLaTeX.com \[1^2+2^2+3^2+\cdots+n^2=\sum_{i=1}^n{i^2}=\frac{n(n+1)(2n+1)}{6}.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-02bcdbdb62193de9ac3fa36c12ec7029_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^n{i^2}=\frac{n(n+1)(2n+1)}{6}\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-ded4f12364f9af442cf21b35c7fe99ff_l3.png)