
Wie die vorstehende Abbildung 1 zeigt, besteht das Experiment am Exponat „Die Kreisfläche“ darin, eine kreisförmige Feder mittels zweier (zunächst vertikal und parallel verlaufender) drehbarer Hebel so aufzubiegen, dass ihre Form in der Endstellung (siehe nachfolgende Abbildung 2) eine Strecke von Punkt ![]() nach Punkt
nach Punkt ![]() darstellt.
darstellt.

Hierbei ist
![]()
die Länge des Umfanges des Kreises, den die Feder ursprünglich bildete. Darüber hinaus gilt: Der Flächeninhalt ![]() des rechtwinkligen Dreieckes
des rechtwinkligen Dreieckes ![]() mit den Eckpunkten
mit den Eckpunkten ![]() ,
, ![]() und
und ![]() (siehe Abbildung 1) ist gleich der halben Kreisfläche, d.h.
(siehe Abbildung 1) ist gleich der halben Kreisfläche, d.h.
![]()
Damit kann der Flächeninhalt ![]() eines Kreises mit dem Radius
eines Kreises mit dem Radius ![]() durch die Summe der Flächeninhalte zweier kongruenter Dreiecke dargestellt werden.
durch die Summe der Flächeninhalte zweier kongruenter Dreiecke dargestellt werden.
Und nun … die Mathematik dazu:
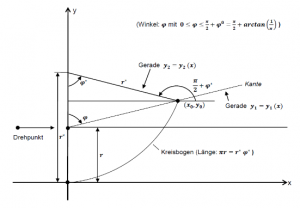
Werden die beiden Hebel jeweils um den Winkel ![]() gegen die vertikale Achse gedreht, so ergibt sich auf der rechten Seite der Berührungspunkt
gegen die vertikale Achse gedreht, so ergibt sich auf der rechten Seite der Berührungspunkt ![]() zwischen dem rechten Hebelarm und dem aufgebogenen Kreis. Letzterer stellt sich nun als Kreisbogen mit dem Radius
zwischen dem rechten Hebelarm und dem aufgebogenen Kreis. Letzterer stellt sich nun als Kreisbogen mit dem Radius ![]() und dem Öffnungswinkel
und dem Öffnungswinkel ![]() (in Bogenmaß!) dar. Somit gilt
(in Bogenmaß!) dar. Somit gilt
![]()
und
![]()
Entsprechend obiger Abbildung 3 gilt für die Geraden ![]() und
und ![]() :
:
![]()
und
![]()
Ihr Schnittpunkt ![]() ergibt sich dann als Lösung der Gleichung
ergibt sich dann als Lösung der Gleichung
![]()
d.h.
![]()
und somit
![]()
Daraus resultiert entsprechend Gleichung (1):
![]()
und somit
![]()
Die Gleichungen (1) und (2) liefern dann
![]()
und somit
![]()
was nach Ausmultiplizieren und Kürzen auf
![]()
führt. Das heißt nun
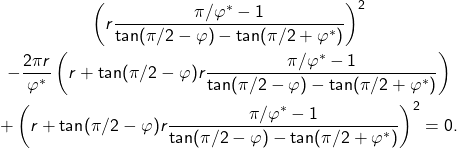
Ohne Einschränkung kann folglich angenommen werden, dass ![]() ist, sodass man für einen gegebenen Öffnungswinkel
ist, sodass man für einen gegebenen Öffnungswinkel ![]() (im Bogenmaß) des rechten Hebels (siehe Abbildung 3) den Öffnungswinkel
(im Bogenmaß) des rechten Hebels (siehe Abbildung 3) den Öffnungswinkel ![]() des entsprechenden Kreisbogens (mit dem Radius
des entsprechenden Kreisbogens (mit dem Radius ![]() ) als Lösung der folgenden Gleichung erhält:
) als Lösung der folgenden Gleichung erhält:
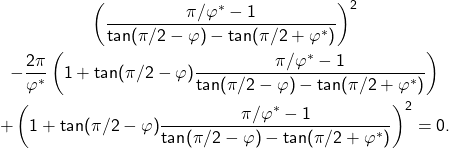
Abschließend geben wir — numerisch als Näherungswerte ermittelt — für ![]() (
(![]() ) die entsprechenden Winkel
) die entsprechenden Winkel ![]() und die Radien
und die Radien ![]() an (mittels der vorstehenden Gleichung).
an (mittels der vorstehenden Gleichung).
| | ||||||
|---|---|---|---|---|---|---|
Tabelle 1: Die Werte ![]() und
und ![]() in Abhängigkeit von
in Abhängigkeit von ![]()
Die nachfolgende Abbildung 4 fasst dies in einem Diagramm zusammen.
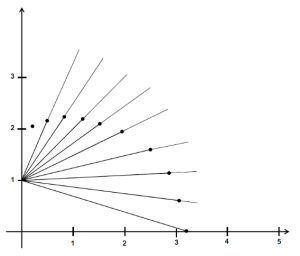
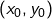 für die verschiedenen Öffnungswinkel zeigt
für die verschiedenen Öffnungswinkel zeigtAnmerkung: Dieses Exponat steht in enger Verbindung zu den Exponaten „Was ist Pi?“, „Wie groß ist die Fläche eines Kreises?“ und „Zwölf Ecken“.
