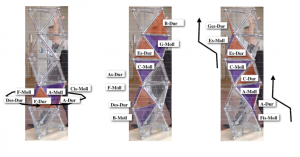
Dreiklangpolyeder
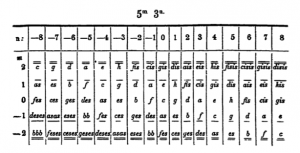
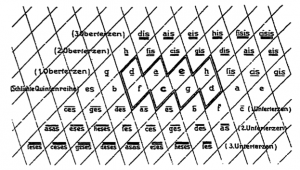
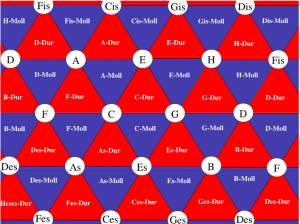
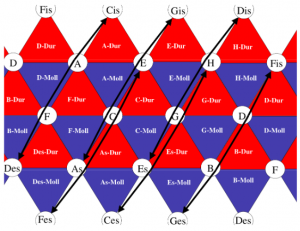
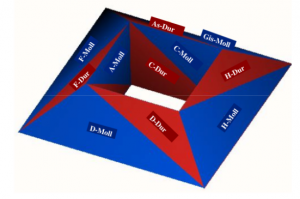
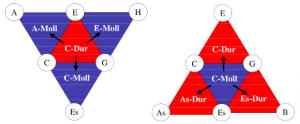
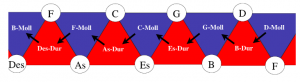
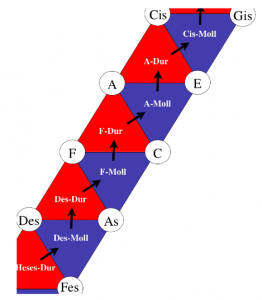
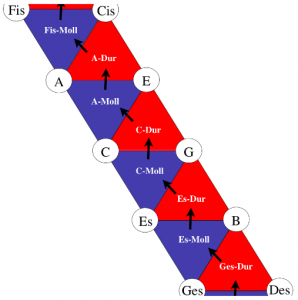
In der Musiktheorie des 19. Jahrhunderts wurden die Verwandtschaftsbeziehungen von Tönen und Dreiklängen mit Hilfe von zweidimensionalen Darstellungen studiert. Folgende Tonverwandtschaftstabelle findet sich in Arthur von Oettingens Abhandlung „Harmoniesystem in dualer Entwicklung“ von 1866. Nebeneinander stehende Töne sind Quint-verwandt und übereinander stehende Töne sind Großterz-verwandt. Oktav-Verwandtschaft wird in dieser zweidimensionalen Darstellung vernachlässigt und wäre bei Bedarf als eine dritte Dimension zu denken.