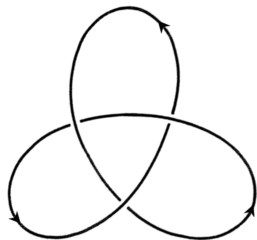
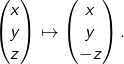Beim „Durchkrabbelknoten“ sind deine akrobatischen Fähigkeiten gefragt. Indem du durch die Metallkonstruktion hindurch krabbelst, folgst du mit deinem Körper einer Knotenlinie. Es handelt sich dabei um die sogenannte linkshändige Kleeblattschlinge. Vermutlich kennen viele diesen Knoten nur als Überhandknoten. Es ist nämlich derjenige Knoten, den wir häufig beim Zubinden der Schnürsenkel nutzen. In der Mathematik besitzen Knoten, die wir aus dem Alltag, Beruf oder Hobby kennen, oftmals einen anderen Namen.

In der Mathematik untersucht man genau dies: Welche Knoten kann man durch endlich viele Schritte ineinander überführen. Es geht also eher weniger um die Funktionalität und das Einsatzgebiet der Knoten. Da man trivialerweise jeden Knoten in einem Strick lösen und wieder einen neuen binden kann, interessiert man sich in der Mathematik nur für solche „Stricke“, bei denen die beiden Enden zusammengeklebt sind. Da außerdem ein Strick ein physisches und kein mathematisches Objekt ist, benötigen wir erst einmal die mathematische Definition eines Knotens und was es heißt, dass zwei Knoten gleich sind bzw. ineinander umgewandelt werden können.
Und nun … die Mathematik
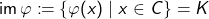 ,
, und
und  sind stetig.
sind stetig.
Eigenschaften von Knoten
- Verdrehung und Entdrehung beider Richtungen,
- Schieben eines Stranges über einen anderen,
- Bewegen eines Strangs über oder unter eine Kreuzung.
Oftmals visualisiert man einen Knoten nicht im ![]() , sondern betrachtet seine Projektion auf die Ebene. Zu diesem Zwecke definieren wir die Abbildung
, sondern betrachtet seine Projektion auf die Ebene. Zu diesem Zwecke definieren wir die Abbildung ![]() mittels
mittels
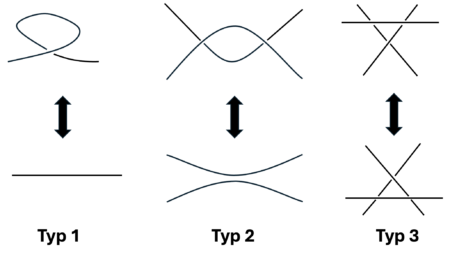
Falls der Knoten eine Orientierung besitzt, dann kann den Überschneidungspunkten eine Händigkeit zugeordnet werden.
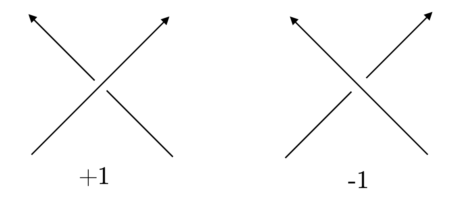
In Abbildung 4 ist der erste Überschneidungpunkt rechtshändig und besitzt das Vorzeichen ![]() und der zweite ist linkshändig und besitzt das Vorzeichen
und der zweite ist linkshändig und besitzt das Vorzeichen ![]() . Der Grund, warum man den Knoten in Abbildung 2 linkshändige Kleeblattschlinge nennt, ist, dass er genau drei linkshändige Überschneidungspunkte besitzt. Sein Spiegelbild, die rechtshändige Kleeblattschlinge, besteht dabei aus drei rechtshändigen Überschneidungspunkten.
. Der Grund, warum man den Knoten in Abbildung 2 linkshändige Kleeblattschlinge nennt, ist, dass er genau drei linkshändige Überschneidungspunkte besitzt. Sein Spiegelbild, die rechtshändige Kleeblattschlinge, besteht dabei aus drei rechtshändigen Überschneidungspunkten.
Äquivalenz von Knoten
Knoteninvarianten
Eine Invariante ist eine universelle Eigenschaft von Knoten, die bei zwei zueinander äquivalenten Knoten gleich bleibt. Falls also ![]() und
und ![]() äquivalente Knoten sind, dann bezeichnen wir eine Abbildung
äquivalente Knoten sind, dann bezeichnen wir eine Abbildung ![]() , die einem Knoten z.B. eine reelle Zahl zuordnet, als Invariante, falls
, die einem Knoten z.B. eine reelle Zahl zuordnet, als Invariante, falls ![]() . Andersherum, falls
. Andersherum, falls ![]() , dann folgt schon, dass
, dann folgt schon, dass ![]() und
und ![]() nicht äquivalent sein können. Eine Invariante ist z.B. die sogenannte Knotengruppe. Sie ist definiert als die Fundamentalgruppe
nicht äquivalent sein können. Eine Invariante ist z.B. die sogenannte Knotengruppe. Sie ist definiert als die Fundamentalgruppe ![]() , also als diejenige Gruppe aller Homotopieklassen auf
, also als diejenige Gruppe aller Homotopieklassen auf ![]() . Oftmals gibt man die Knotengruppe über eine Präsentation an, also als eine Darstellung von Erzeugern und Relationen. Hierbei sind die Relationen genau die Überschneidungspunkte des Knotendiagramms. Die Fundamentalklasse der Kleeblattschlinge besitzt z.B. die Präsentation
. Oftmals gibt man die Knotengruppe über eine Präsentation an, also als eine Darstellung von Erzeugern und Relationen. Hierbei sind die Relationen genau die Überschneidungspunkte des Knotendiagramms. Die Fundamentalklasse der Kleeblattschlinge besitzt z.B. die Präsentation
Oftmals genügt es, eine Knoteninvariante nur auf Knotendiagrammen zu definieren. Stimmt nämlich eine solche Invariante bei zwei unterschiedlichen Knotendiagrammen nicht überein, dann können diese nicht durch Reidemeister Bewegungen ineinander umgewandelt werden, sprich sie repräsentieren jeweils einen anderen Knoten. Es gibt dabei viele verschiedene Arten von Invarianten.
Kreuzungszahl. Eine offensichtliche Invariante ist die minimale Anzahl von Überschneidungspunkten im Knotendiagramm, die durch Reidemeister Bewegungen erreichbar ist. Haben nämlich zwei Knoten eine verschiedene Kreuzungszahl, dann müssen sie schon einen anderen Knoten repräsentieren. Bei der Kleeblattschlinge beträgt die Kreuzungszahl genau ![]() . Überlege dir, warum jeder Knoten mit der Kreuzungszahl 1 und 2 schon der triviale Knoten sein muss.
. Überlege dir, warum jeder Knoten mit der Kreuzungszahl 1 und 2 schon der triviale Knoten sein muss.
Windungszahl. Eine weitere Invariante von Knoten ist die Summe der Vorzeichen aller Überschneidungspunkte. So besitzt die linkshändige Kleeblattschlinge die Windungszahl -3 und ihr rechtshändiges Pendant die Windungszahl +3. Im Speziellen ist jeder Knoten mit Windungszahl kleiner als ![]() äquivalent zum Unknoten.
äquivalent zum Unknoten.
Chiralität. Ein chiraler Knoten kann nicht äquivalent zu einem Knoten sein, der auch äquivalent zu seinem Spiegelbild ist.
Literatur
- Lickorish, W. B. Raymond: An Introduction to Knot Theory, Springer, 1963
- Adams, Colin Conrad Adams, Colin Conrad: The knot book an elementary introduction to the mathematical theory of knots, American Mathematical Society, 2004

![Rendered by QuickLaTeX.com \begin{align*}\begin{pmatrix}x \\ y \\ z\end{pmatrix}= \begin{pmatrix}(2 + \cos 3t) \cos 2t \\(2 + \cos 3t) \sin 2t \\\sin 3t\end{pmatrix},&& t \in [0,2\pi].\end{align*}](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-0090bc6792bf693a5cad56bf5370136f_l3.png)