Stell dir vor, du möchtest kreisrunde Plätzchen backen. Du bereitest den Teig vor und rollst ihn aus. Für das Ausstechen hast du aber nur einen Versuch. Deine Aufgabe ist also, so viele Plätzchen wie möglich aus dem Teig auszustechen, ohne dabei Teig zu verschwenden. Aber wie könnte eine optimale Lösung dieses Problems aussehen? Du wirst schnell feststellen, dass es in Abhängigkeit von der Fläche und Form des ausgerollten Teiges und der Größe deiner Ausstechform eine Anzahl von Keksen gibt, die du höchstens aus dem Teig ausstechen kannst. Aber selbst wenn du diese Zahl kennen würdest, ist es nicht klar, in welcher Anordnung du sie ausstechen musst.

Bei unserem Exponat „Pferch“ kannst du genau dies untersuchen. Auf unserem Exponatstisch findest du 7 Spielflächen, in denen du die dort angegebene Anzahl an Spielmünzen in die umrandeten Formen „einpferchen“ musst. Die Lösung ist dabei oft viel weniger symmetrisch, als man zuerst denken würde. In der Mathematik ist dieses Problem verwandt mit dem sogenannten „Kugelpackungsproblem“. Dabei ist die Aufgabe, die dichteste Kugelpackung, also die effizienteste Anordnung gleich großer Kugeln zu finden, die sich höchstens berühren und einen minimalen Zwischenraum lassen. Seinen Ursprung findet das Problem in der Frage nach der dichtesten Anordnung von Kanonenkugeln. Im Jahre 1611 stellte Johannes Kepler die Vermutung auf, dass die dichteste Kugelpackung das hexagonale Gitter ist, welches du in Abbildung 2 erkennen kannst. Jedoch konnte erst im Jahre 1831 von Carl Friedrich Gauß bewiesen werden, dass dies tatsächlich die effizienteste Anordnung ist.
Und nun … die Mathematik
Im Folgenden wollen wir uns mit dem Kugelpackungsproblem im zweidimensionalen euklidischen Raum ![]() beschäftigen. In diesem Fall sind die Kugeln Kreisscheiben. Außerdem ist das Problem zur Auffindung der dichtesten Kugelpackung abhängig davon, ob die Fläche, in der wir die Kreisscheiben anordnen wollen, einen Rand hat, oder unbeschränkt ist. Beim Exponat Pferch soll eine bestimmte Anzahl der Scheiben in ein Quadrat, einen Kreis oder ein Dreieck eingefügt werden. Die Lösung hierbei ist aber viel weniger symmetrisch als wenn man die Scheiben auf einem unberandeten Gebiet möglichst dicht anordnen möchte. Wir studieren im Folgenden beide Fragestellungen.
beschäftigen. In diesem Fall sind die Kugeln Kreisscheiben. Außerdem ist das Problem zur Auffindung der dichtesten Kugelpackung abhängig davon, ob die Fläche, in der wir die Kreisscheiben anordnen wollen, einen Rand hat, oder unbeschränkt ist. Beim Exponat Pferch soll eine bestimmte Anzahl der Scheiben in ein Quadrat, einen Kreis oder ein Dreieck eingefügt werden. Die Lösung hierbei ist aber viel weniger symmetrisch als wenn man die Scheiben auf einem unberandeten Gebiet möglichst dicht anordnen möchte. Wir studieren im Folgenden beide Fragestellungen.

Dichteste Kugelpackung bei beschränkten Flächen
Quadrat
(1) ![]()
(2) ![]()
![]()
![]()
![]()

 Kugeln im Einheitsquadrat
Kugeln im EinheitsquadratDie optimale Anordnung für ![]() kannst du in Abbildung 3 sehen. Hier ist die Lösung noch sehr symmetrisch. Falls die Anzahl der Kreise
kannst du in Abbildung 3 sehen. Hier ist die Lösung noch sehr symmetrisch. Falls die Anzahl der Kreise ![]() aber größer wird, werden die Anordnungen jedoch alles andere als symmetrisch bzw. sind noch gar keine (optimalen) Lösungen bewiesen wurden. Bis jetzt konnte eine optimale Anordnung für
aber größer wird, werden die Anordnungen jedoch alles andere als symmetrisch bzw. sind noch gar keine (optimalen) Lösungen bewiesen wurden. Bis jetzt konnte eine optimale Anordnung für ![]() gezeigt werden und für
gezeigt werden und für ![]() ist eine nicht notwendigerweise optimale Lösung bekannt. In der untenstehenden Tabelle findest du die Radien und das Verhältnis
ist eine nicht notwendigerweise optimale Lösung bekannt. In der untenstehenden Tabelle findest du die Radien und das Verhältnis ![]() aus (2) für
aus (2) für ![]() .
.
| Anzahl | Radius | Verhältnis |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Übrigens ist die quadratische Anordnung, welche bei ![]() optimal ist, auch optimal bei
optimal ist, auch optimal bei ![]() , also genau wenn
, also genau wenn ![]() eine der ersten sechs Quadratzahlen ist. Jedoch ist die quadratische Anordnung für
eine der ersten sechs Quadratzahlen ist. Jedoch ist die quadratische Anordnung für ![]() ineffizient.
ineffizient.
Kreis
![]()
![]()

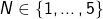 Kugeln im Einheitskreis
Kugeln im EinheitskreisIn der obigen Abbildung kannst du die optimale Anordnung für ![]() Kreise im Einheitskreis sehen. Übrigens gibt es für
Kreise im Einheitskreis sehen. Übrigens gibt es für ![]() zwei optimale Lösungen, wie du in Abbildung 5 erkennen kannst.
zwei optimale Lösungen, wie du in Abbildung 5 erkennen kannst.

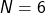 Kugeln im Einheitskreis
Kugeln im EinheitskreisBis jetzt konnte eine optimale Anordnung für ![]() bewiesen werden. Für
bewiesen werden. Für ![]() konnte bis jetzt nur eine optimale Anordnung vermutet werden. In der unten stehenden Tabelle findest du die Radien und das Verhältnis
konnte bis jetzt nur eine optimale Anordnung vermutet werden. In der unten stehenden Tabelle findest du die Radien und das Verhältnis ![]() für
für ![]() .
.
| Anzahl | Radius | Verhältnis |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Gleichseitiges Dreieck
Abschließend betrachten wir ein gleichseitiges Dreieck mit Seitenlänge ![]() , für welches wir eine größtmögliche Zahl
, für welches wir eine größtmögliche Zahl ![]() bestimmen wollen, sodass
bestimmen wollen, sodass ![]() Kreise mit Radius
Kreise mit Radius ![]() in dieses Dreieck passen. Kannst du zeigen, dass diese Fragestellung äquivalent dazu ist, eine minimale Seitenlänge
in dieses Dreieck passen. Kannst du zeigen, dass diese Fragestellung äquivalent dazu ist, eine minimale Seitenlänge ![]() für ein gleichseitiges Dreieck anzugeben, sodass
für ein gleichseitiges Dreieck anzugeben, sodass ![]() Einheitskreise hinein passen?
Einheitskreise hinein passen?

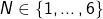 Kugeln in einem gleichseitigen Dreieck mit Seitenlänge 1
Kugeln in einem gleichseitigen Dreieck mit Seitenlänge 1In Abbildung 6 kannst du die optimale Anordnung für ![]() erkennen. Bis zum heutigen Tage wurde nur für
erkennen. Bis zum heutigen Tage wurde nur für ![]() eine optimale Packung gefunden. Paul Erdös behauptete, dass, falls
eine optimale Packung gefunden. Paul Erdös behauptete, dass, falls ![]() eine Dreieckszahl ist, der maximale Radius
eine Dreieckszahl ist, der maximale Radius ![]() bzw. die minimale Seitenlänge
bzw. die minimale Seitenlänge ![]() bei
bei ![]() und
und ![]() Kreisscheiben gleich sind. Für die ersten Fälle
Kreisscheiben gleich sind. Für die ersten Fälle ![]() kannst du dich in der unten stehenden Tabelle selbst überzeugen.
kannst du dich in der unten stehenden Tabelle selbst überzeugen.
| Anzahl | Radius | Verhältnis |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Dichteste Kugelpackung im 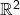
Ein gänzlich anderes Problem ist eine dichteste Packung für Einheitskreise in der gesammten euklidischen Ebene ![]() zu finden. Anstelle einer endlichen Fläche, wie bei den Beispielen oben, ist die Fläche des
zu finden. Anstelle einer endlichen Fläche, wie bei den Beispielen oben, ist die Fläche des ![]() unendlich. Wir müssen demnach unendlich viele Kreise auf einer unendlich großen Fläche so platzsparend wie möglich anordnen. Man kann sich leicht vorstellen, dass die Aufgabe sehr schwierig ist, unter allen möglichen Anordnungen diejenige Packung zu finden, die am dichtesten ist. Selbst wenn man eine Vermutung hat, ist es nicht trivial zu beweisen, dass sie unter allen Möglichkeiten auch die dichteste ist.
unendlich. Wir müssen demnach unendlich viele Kreise auf einer unendlich großen Fläche so platzsparend wie möglich anordnen. Man kann sich leicht vorstellen, dass die Aufgabe sehr schwierig ist, unter allen möglichen Anordnungen diejenige Packung zu finden, die am dichtesten ist. Selbst wenn man eine Vermutung hat, ist es nicht trivial zu beweisen, dass sie unter allen Möglichkeiten auch die dichteste ist.
![]()
![]()
![]()
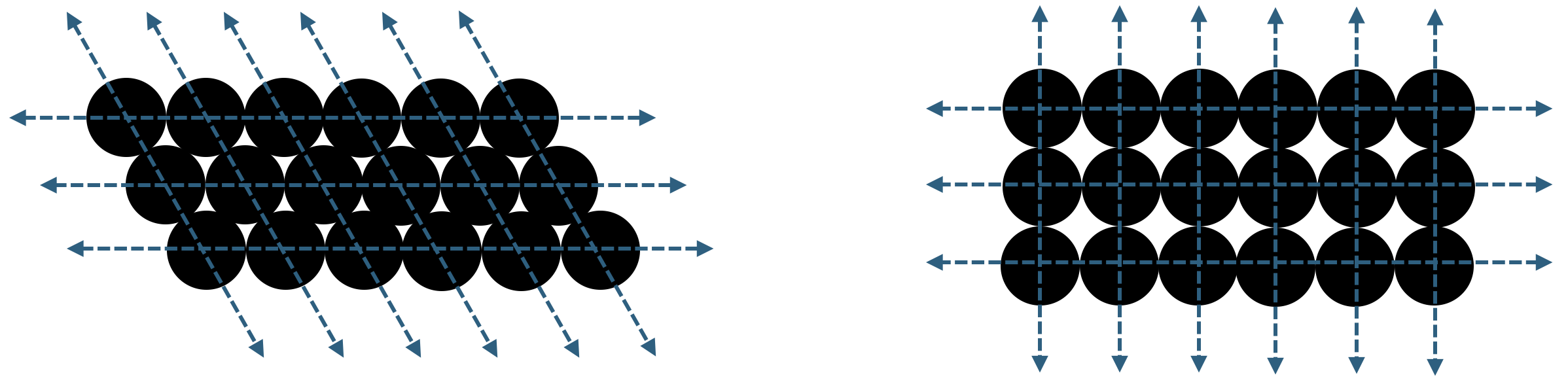
Es sei bemerkt, dass man das Kugelpackungsproblem allgemein in ![]() für jede Dimension
für jede Dimension ![]() formulieren kann. Bis jetzt sind nur optimale Packungen für
formulieren kann. Bis jetzt sind nur optimale Packungen für ![]() bekannt.
bekannt.
Unser Logo: Die Biesterformen
In Abbildung 7 und 8 kannst du erkennen, dass jeder Kreis im hexagonalen Gitter 6 benachbarte Zwischenräume besitzt. Wählt man ein paar davon aus und „klebt“ sie an den Kreis, erhält man bis auf Kongruenz insgesamt 13 verschiedene Formen, die du in Abbildung 9 erkennen kannst.
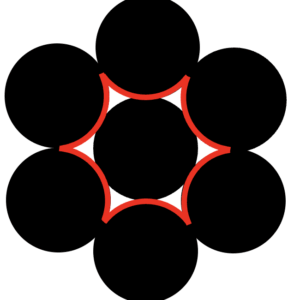
Unser Logo besteht genau aus diesen 13 verschiedenen Formen. Da sie sich nur widerspenstig zusammensetzen lassen, ist der Name „Biester“ entstanden. Beim Exponat „Biesterhocker“, welches sich am Eingangsbereich befindet, kannst du dich selbst einmal darin versuchen, unser Logo zusammenzusetzen. Es gibt übrigens über 20 000 verschiedene Möglichkeiten, dies zu tun.

Es ist auch möglich, eine zusammenhängende Fläche im ![]() mit den Biesterformen zu überdecken. Jedoch kann man zeigen, dass es nicht möglich ist, alle Teile dabei gleich häufig zu verwenden.
mit den Biesterformen zu überdecken. Jedoch kann man zeigen, dass es nicht möglich ist, alle Teile dabei gleich häufig zu verwenden.
Literatur
- https://en.wikipedia.org/wiki/Packing_problems
- https://en.wikipedia.org/wiki/Packing_problems
- Abbildung 2: https://www.spektrum.de/kolumne/keplersche-vermutung-wie-ein-pirat-die-mathematik-praegte/2096145
