Pythagoras zum Legen

Bei diesem Exponat geht es um einen weiteren anschaulichen Beweis des Satzes des Pythagoras. Der bekannte Lehrsatz besagt, dass die Seitenlängen $a$ , $b$ und $c$ eines rechtwinkligen Dreiecks die Gleichung $a^2+b^2=c^2$ erfüllen (wobei $a$ und $b$ die beiden Seiten sind, die den rechten Winkel einschließen, — die sogenannten Katheten — und $c$ die gegenüberliegende Seite ist — die Hypotenuse).

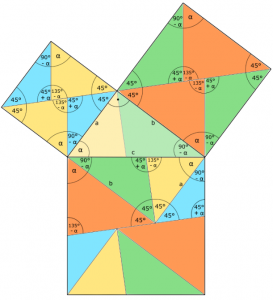
Dieses Mal ist der Beweis in Form eines Puzzles gegeben, dass der Besucher selbst lösen muss, um ihn nachzuvollziehen: Über den Katheten befinden sich zwei in jeweils vier Dreiecke zerlegte Quadrate. Jedes dieser Dreiecke ist gefärbt und die beiden gegenüberliegenden Dreiecke im Quadrat sind jeweils kongruent („deckungsgleich“) und gleich gefärbt.

Legt man nun die insgesamt acht Dreiecke geschickt um, so füllen diese genau das Quadrat über der Hypotenuse aus (siehe Abbildung 1). Damit ist der Satz des Pythagoras bewiesen, denn aus Zerlegungsgleichheit folgt Inhaltsgleichheit.

Weiteres Wissenswertes zum Satz des Pythagoras und einen weiteren Beweis findest Du hier.

Literatur

[1] Dewdney, A.K.: Reise in das Innere der Mathematik, Berlin, 2000.

[2] Fraedrich, A.M.: Die Satzgruppen des Pythagoras, Mannheim, 1995.

[3] Maor, E.: The Pythagorean Theorem: A 4,000-year History, Princeton, 2007.

[4] Schupp, H.: Elementargeometrie, Stuttgart, 1977.

[5] Singh, S.: Fermats letzter Satz, München, 2000.

[6] v. Wedemeyer, I.: Pythagoras, Weisheitslehrer des Abendlandes, Ahlerstedt, 1988.