Taklamakan
Da steht man auf einem Aussichtspunkt, schaut hinunter ins Tal und fragt sich vielleicht: Wie steil war eigentlich der Weg hier rauf? Oder: Warum fließt der Bach genau da entlang und nicht woanders? Wer eine Wanderkarte zur Hand hat, sieht dort kurvige Linien, die sich über die Landschaft ziehen: sogenannte Höhenlinien. Je enger sie beieinanderliegen, desto steiler ist das Gelände. Aber wie entstehen diese Linien eigentlich und was sagen sie wirklich über die Landschaft aus?


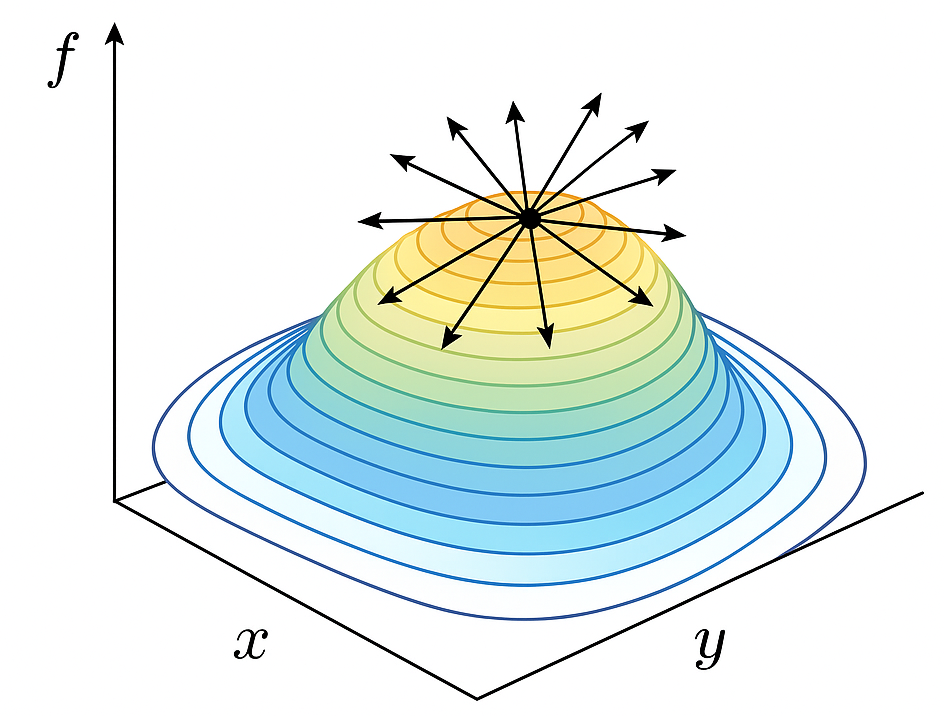
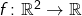 und verschiedene Ableitungsrichtungen in einem Punkt
und verschiedene Ableitungsrichtungen in einem Punkt