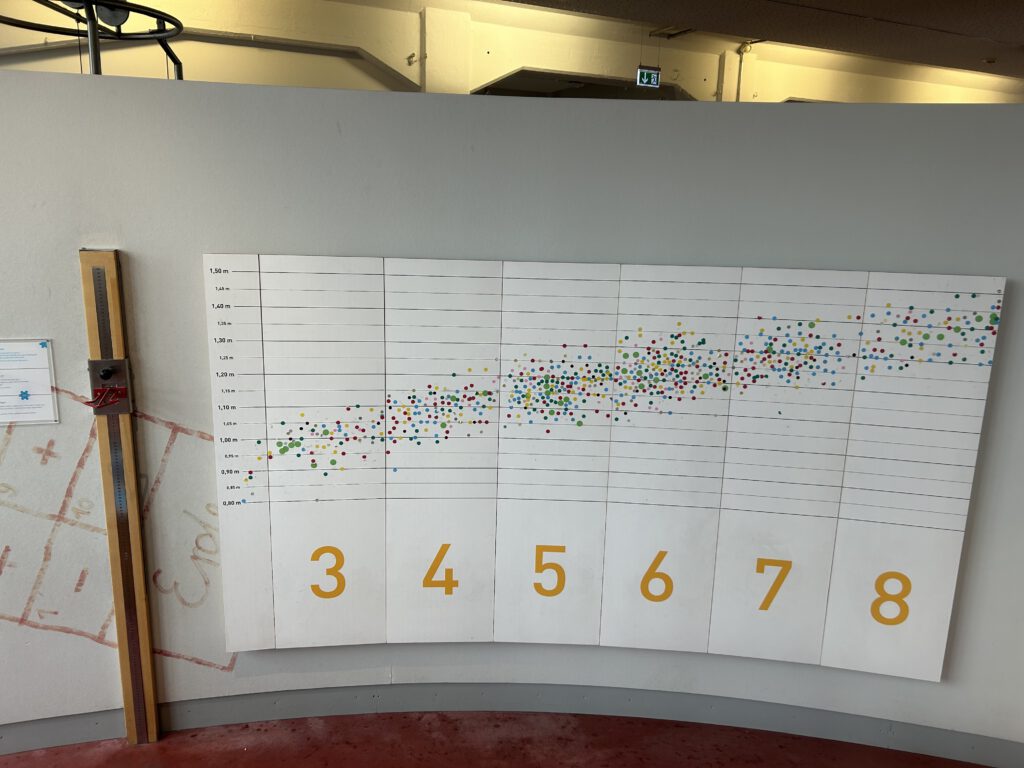
Wie Groß bin ich?

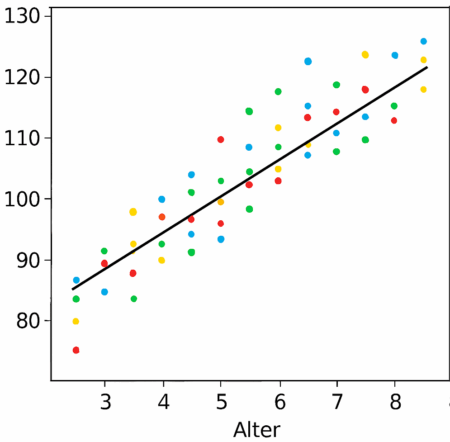
Hast du dich schon einmal gefragt, ob du größer oder kleiner bist als andere in deinem Alter? Vielleicht hat jemand in deiner Klasse gesagt: „Ich bin schon 1,30 Meter groß, wie groß bist du eigentlich?“ Genau solche Vergleiche macht dieses Exponat sichtbar. Mit dem Schieber misst du deine Größe und klebst einen Punkt auf die Tafel, genau dort, wo dein Alter steht. So wächst aus vielen einzelnen Datenpunkten ein beeindruckendes Bild: eine bunte „Wolke“ aus Körpergrößen.

Und nun … die Mathematik

Körpergrößen sind ein typisches Beispiel für sogenannte Zufallsgrößen – also Messwerte, die in einer Population nicht konstant, sondern unterschiedlich verteilt sind. Auch wenn alle 6-jährigen Kinder in etwa gleich alt sind, unterscheiden sie sich in ihrer Größe: Manche sind überdurchschnittlich groß, andere etwas kleiner. Die Frage ist: Wie sind diese Werte insgesamt verteilt? Und wie stark streuen sie um den Mittelwert?

Die Antwort gibt die Normalverteilung, eines der wichtigsten Modelle in der Statistik. Sie beschreibt viele natürliche Phänomene – von Körpergrößen über Blutdruck bis hin zu Messfehlern. Die typische Glockenform des Graphens ihrer Wahrscheinlichkeitsdichtefunktion zeigt, dass die meisten Werte in der Nähe des Durchschnitts liegen, extreme Abweichungen nach oben oder unten jedoch seltener sind. Ihre Abbildungsvorschrift ist gegeben durch

$f(x) \coloneqq \frac{1}{\sigma \sqrt{2\pi}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right).$

Dabei ist:

$x$ : die Körpergröße,
$\mu$ : der Mittelwert, also die durchschnittliche Körpergröße in einer Altersgruppe,
$\sigma$ : die Standardabweichung, die angibt, wie stark die Größen um den Mittelwert streuen.

Die Verteilungsfunktion $F(x)$ beschreibt, wie viel Prozent der gemessenen Werte $X$ kleiner oder gleich $x$ sind:

$F(x) = P(X \leq x)$

Sie ist besonders hilfreich, wenn man Fragen wie diese beantworten will: „Wie viele Kinder sind kleiner als 1,20m?“ oder „Wie groß ist der Anteil besonders großer Kinder?“.

Auf dem Exponat sieht man diese Verteilung bildlich: Jeder Punkt steht für ein Kind. Je mehr Punkte in einem Bereich, desto häufiger kommt diese Körpergröße in dieser Altersstufe vor. Die Breite der Verteilung zeigt die Streuung – und damit indirekt auch die Standardabweichung.

Doch es geht noch weiter: Wenn man alle Punkte betrachtet, erkennt man eine steigende Tendenz – je älter das Kind, desto größer ist es im Durchschnitt. Dies lässt sich mathematisch durch eine lineare Regression erfassen: eine Gerade, die möglichst gut durch alle Punkte „hindurchpasst“. Die Steigung dieser Regressionsgeraden (siehe Abbildung 2) zeigt, wie stark Kinder im Durchschnitt pro Jahr wachsen.

Beispiel: Liegt die Steigung der Regressionsgeraden bei etwa 6,5 cm pro Jahr, bedeutet das: Zwischen 3 und 8 Jahren wächst ein Kind im Mittel um genau diesen Betrag – unabhängig von Schwankungen im Einzelfall.

Diese mathematischen Werkzeuge – Normalverteilung, Mittelwert, Standardabweichung und Regression – helfen nicht nur dabei, Wachstumsverläufe zu beschreiben. Sie zeigen auch, wie Mathematik die Vielfalt des Lebens in strukturierte Modelle übersetzt – und dabei Raum für individuelle Unterschiede lässt.