Würfelschnitte
Dieses Exponat steht im ![]() psilon, dem Erlebnisland für Kleine.
psilon, dem Erlebnisland für Kleine.
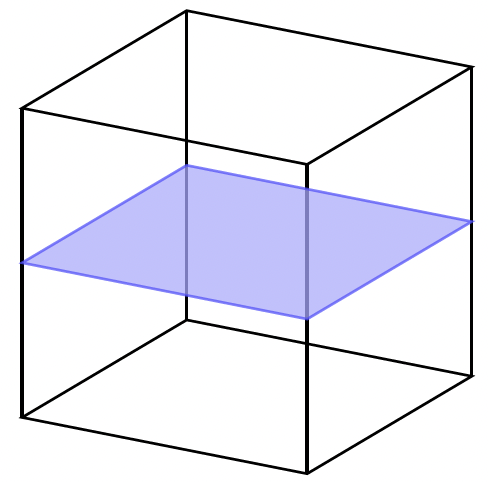
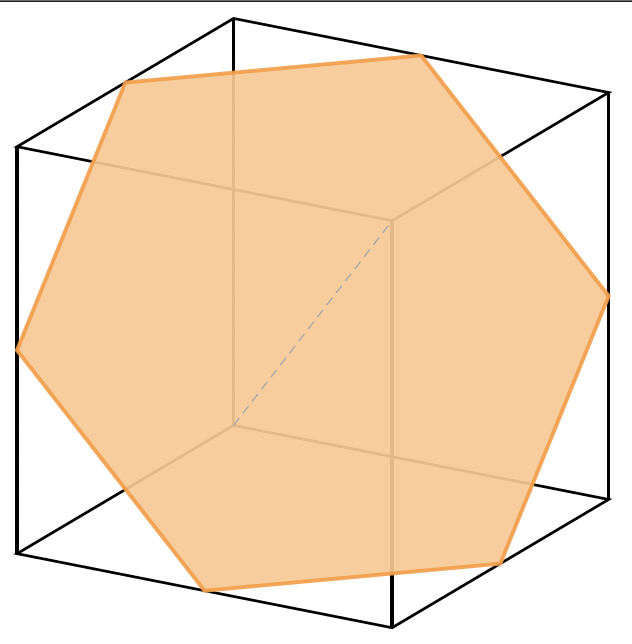
Stell dir vor, du schneidest ein Stück Kuchen an. Je nachdem, wie du das Messer ansetzt, erhältst du ein spitzes Dreieck, ein Rechteck oder ein Trapez. Mit einer Melone passiert das Gleiche: Mal entstehen dünne Scheiben, mal große Stücke, die ganz unterschiedlich aussehen.
Genau dieses Phänomen macht sich das Exponat „Würfelschnitte“ zunutze. Ein Würfel, den wir sonst nur mit seinen Kanten und Flächen wahrnehmen, wird hier in verschiedene Scheiben zerteilt. Die einzelnen Stücke wirken zunächst merkwürdig: Manche haben dreieckige Flächen, andere viereckige oder sogar sechseckige. Auf den ersten Blick würde man kaum glauben, dass all diese Formen zusammen einmal einen ganz normalen Würfel ergeben.
Die Aufgabe im Exponat lautet deshalb: Setze die Bausteine wieder zu zwei Würfeln zusammen. Dabei wird schnell klar: Was wie ein chaotisches Durcheinander aussieht, folgt einer klaren geometrischen Ordnung.