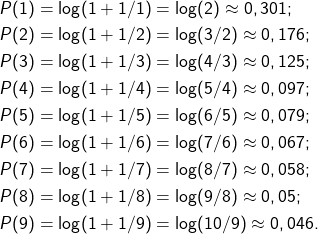Benford’s Law

In 1881, the American mathematician Simon Newcomb noticed that in the logarithm tables used by his students, the pages with logarithms beginning with the digit “1” had more “dog-ears” than the following pages on which the logarithms with “2”, “3”, “4”, etc. came first. However, his mathematical description of this phenomenon in the American Journal of Mathematics was quickly forgotten.

It was not until 1937 that this law was rediscovered by the physicist Frank Benford (1883–1948), studied on the basis of over 20,000 data and systematically analysed. The law subsequently named after him states — formulated mathematically — that if a number is selected at random from a table of physical constants or statistical data, the probabilityof the first digit being a “1” is about 0.301. It is therefore far greater than 0.1, the value one might expect if all digits were equally likely to occur. In general, Benford’s law says about the probability that the first digit equals “ $k$ “:

$P( {k} )=\log(1+1/k).$

Here $\log$ denotes the decadic logarithm and $k$ can take the values 1, 2, …, 9. In detail, this results in:

$\begin{align*}P({1}) &= \log(1+1/1)=\log(2)\approx 0,301;\\ P({2}) &= \log(1+1/2) = \log(3/2)\approx 0,176;\\ P({3}) &= \log(1+1/3) = \log(4/3)\approx 0,125; \\ P({4}) &= \log(1+1/4) = \log(5/4)\approx 0,097; \\ P({5}) &= \log(1+1/5)=\log(6/5)\approx 0,079; \\ P({6}) &= \log(1+1/6)=\log(7/6)\approx 0,067; \\ P({7}) &= \log(1+1/7)=\log(8/7)\approx 0,058;\\ P({8}) &= \log(1+1/8)=\log(9/8)\approx 0,05;\\ P({9}) &= \log(1+1/9)=\log(10/9)\approx 0,046.\end{align*}$

Consequently, Benford’s law implies that a number with a “smaller” first digit is more likely to occur in a table of statistical data than a number with a “larger” first digit. Benford’s Law is applied in the detection of fraud in the preparation of financial statements, falsification in accounts, generally for the rapid detection of blatant irregularities in accounting. With the help of Benford’s Law, the remarkably “creative” accounting at ENRON, the largest American company in the energy industry at the time (with 22,000 employees), was uncovered in 2001, through which the management had defrauded investors of their deposits to the tune of about 30 billion dollars. Nowadays, auditors, tax investigators and even election observers use mathematical-statistical methods to detect forgeries in the event of conspicuous deviations from the Benford distribution.

By means of the exhibit in the Maths Adventure Land, Benford’s Law can be reproduced experimentally with frequencies of spheres lying on top of each other (see Figure 1 above). Suitable panels of random numbers are available to choose from for the experiment.

And now … the mathematics:

The starting point for Benford’s law is Newcomb’s so-called mantissa law:

“The frequency of numbers is such that the mantissas of their logarithms are equally distributed.”

The mantissa of a positive number is understood as its so-called fractal part. For a positive real number $x$ , the mantissa of $x$ is equal to $\langle x\rangle\coloneqq x-\lfloor x\rfloor$ (e.g. $\langle 3.1415\rangle=3.1415-\lfloor 3.1415\rfloor=3.1415-3=0.1415$ ).

Now suppose that a set of randomly chosen numbers satisfies the above mantissa law and consider the following sets:

$E_i\coloneqq\{x > 0 \mid \text{the leading digit of $x$ is $i$}\}.$

Then the following applies: The set $\mathbb R_+$ of the positive real numbers is the union of the (element-unrelated) sets $E_i$ , i.e.

$\mathbb R_+=E_1\cup E_2\cup\cdots\cup E_9.$

Thus, for the probability $P$ (probability) that any of the considered random numbers $X$ belongs to the set $E_i$ we get:

$P({X\in E_i})=P(\langle\log(X)\rangle\in[\log(i),\log(i+1)))=\log(i+1)-\log(i)=\log(1+1/i).$

Literature

[1] Benford, F.: The Law of Anomalous Numbers, Proceedings of the American Philosophical Society 78, S. 551–572, 1938.

[2] Glück, M.: Die Benford-Verteilung — Anwendung auf reale Daten der Marktforschung, Diplomarbeit TU Dresden, Betreuer: V. Nollau und H.-O. Müller, 2007.

[3] Newcomb, S.: Note on the Frequency of the Use of different Digits in Natural Numbers, American Journal of Mathematics 4, S. 39–40, 1881.