Circle and Ellipse
An ellipse ![]() is the set of all points
is the set of all points ![]() of the
of the ![]() -plane for which the sum of the distances to two given points
-plane for which the sum of the distances to two given points ![]() and
and ![]() is equal (
is equal (![]() ). Ellipses belong to the class of conic sections (see the exhibit “Conic Sections“)
). Ellipses belong to the class of conic sections (see the exhibit “Conic Sections“)
An ellipse ![]() is the set of all points
is the set of all points ![]() of the
of the ![]() -plane for which the sum of the distances to two given points
-plane for which the sum of the distances to two given points ![]() and
and ![]() is equal (
is equal (![]() ). Ellipses belong to the class of conic sections (see the exhibit “Conic Sections“)
). Ellipses belong to the class of conic sections (see the exhibit “Conic Sections“)
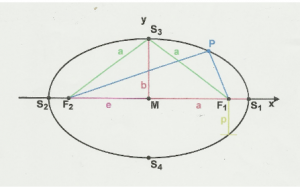
The points ![]() and
and ![]() are called focal points. The centre
are called focal points. The centre ![]() of their connecting line (of length
of their connecting line (of length ![]() ,
, ![]() — eccentricity) is called the centre of the ellipse. The distance from this centre
— eccentricity) is called the centre of the ellipse. The distance from this centre ![]() to the two vertices
to the two vertices ![]() and
and ![]() is
is ![]() in each case and to the vertices
in each case and to the vertices ![]() and
and ![]() is
is ![]() in each case with
in each case with ![]() (according to the Pythagorean theorem; see also the exhibit “Proof without words: Pythagoras for laying“), i.e.
(according to the Pythagorean theorem; see also the exhibit “Proof without words: Pythagoras for laying“), i.e. ![]() .
.
The connecting line between a focal point ![]() or
or ![]() (focus) and a point of the ellipse is called the guide ray or focal ray. The names focal point and focal ray result from the property that the angle between the two focal rays at one point of the ellipse is bisected by the normal (straight line, perpendicular to the tangent) at that point. Thus, the angle of incidence that one focal ray forms with the tangent is equal to the angle of divergence that the tangent forms with the other focal ray. Consequently, a light ray emanating from one focal point, e.g.
(focus) and a point of the ellipse is called the guide ray or focal ray. The names focal point and focal ray result from the property that the angle between the two focal rays at one point of the ellipse is bisected by the normal (straight line, perpendicular to the tangent) at that point. Thus, the angle of incidence that one focal ray forms with the tangent is equal to the angle of divergence that the tangent forms with the other focal ray. Consequently, a light ray emanating from one focal point, e.g. ![]() , is reflected at the elliptical tangent in such a way that it hits the other focal point. With an elliptical mirror, all light rays emanating from one focal point therefore meet at the other focal point. If the eccentricity
, is reflected at the elliptical tangent in such a way that it hits the other focal point. With an elliptical mirror, all light rays emanating from one focal point therefore meet at the other focal point. If the eccentricity ![]() , then
, then ![]() applies. Die Ellipse wird zu einem Kreis mit dem Radius
applies. Die Ellipse wird zu einem Kreis mit dem Radius ![]() .
.
A simple way to draw an ellipse accurately is the so-called gardener’s construction. It directly uses the ellipse definition:
To create an elliptical flower bed, drive two stakes into the focal points and attach the ends of a string of length ![]() to them. Now stretch the string and run a marking device along it. Since this method requires additional tools besides a circle and a ruler – a string – it is not a construction of classical geometry. In ADVENTURE LAND MATHEMATICS, this construction can be understood by means of a simple experiment.
to them. Now stretch the string and run a marking device along it. Since this method requires additional tools besides a circle and a ruler – a string – it is not a construction of classical geometry. In ADVENTURE LAND MATHEMATICS, this construction can be understood by means of a simple experiment.

In the following, the ellipse equation is derived from the “gardener’s construction” described above:
For a point ![]() of the ellipse — according to figure 1 above —
of the ellipse — according to figure 1 above — ![]() , i.e. if we set
, i.e. if we set ![]() and
and ![]() , we get the equation
, we get the equation
![]()
Squaring this equation gives
![]()
and thus
![]()
Squaring again gives:
![]()
and by simplification — i.e. suitable “shortening” — we get:
![]()
i.e.
![]()
Because of ![]() (see above), the normal form (also “midpoint form“) of an elliptic equation is
(see above), the normal form (also “midpoint form“) of an elliptic equation is
![]()
The so-called first Kepler’s law (“ellipse theorem“, “planet theorem“) states that the orbit of a satellite is an ellipse. One of their focal points is in the centre of gravity of the system. This law results from Newton’s law of gravitation, provided that the mass of the central body is considerably greater than that of the satellites and the interaction of the satellite with the central body can be neglected. Consequently, according to Kepler’s first law, all planets move in an elliptical orbit around the sun, with the sun at one of the two foci. The same applies to the orbits of recurring (periodic) comets, planetary moons or double stars.
[1] Schupp, H.: Kegelschnitte, Mannheim, 1988.