Cone Sections

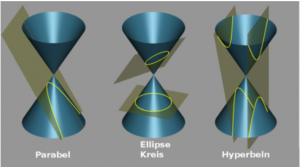
A cone section is a plane curve that results when the surface of a double circular cone is intersected with a plane (cf. Figure 1).

The double circular cone is created by rotating a straight line $g$ around an intersecting axis $h.$ The mantle of the cone then consists of the totality of all straight lines (the so-called surface lines) that result from the very rotation of $g$ around $h.$ The position of the intersection surface in relation to the lateral surfaces determines which conic section is created.

If the tip of the double cone is not in the respective section plane, the following curves can arise:

A parabola is created when the intersection plane is parallel to exactly one generatrix of the double cone. This means that the angle between the axis $h$ and the section plane is equal to half the opening angle of the double cone.

An ellipse occurs when the section plane is not parallel to any surface line. This means that the angle between the axis $h$ and the section plane is greater than half the opening angle of the double cone. If this angle is a right angle, the circle appears as an intersection curve (as a special case of an ellipse).

A hyperbola is created when the intersection plane is parallel to two generatrixes of the double cone. This means that the angle between the axis and the plane is smaller than half the opening angle.

If you use a simple cone instead of a double cone and intersect it with a plane so that the plane does not pass through its apex, you get either a parabola, an ellipse or a branch of a hyperbola, analogous to the three cases just mentioned. Of course, the intersection of such a plane with the cone can also be empty.

In the ADVENTURE LAND MATHEMATICS, the conic sections just mentioned are generated by the following experiment:

A blue coloured liquid is contained in a transparent cone-shaped container whose main axis can be tilted (by hand) up to 90°. If you now set an arbitrary angle, the boundary line of the liquid in this container forms a conic section.

And now … the mathematics:

We now consider the algebraic aspect of conic sections. In the plane Cartesian coordinate system, the general quadratic equations

$ax^2+2bxy+cy^2+2dx+2ey+f=0$

describe (with real coefficients $a,b,c,d,e$ and $f$ ) exactly the conic sections as the zero sets of such equations.

Such an equation can also be written in matrix notation as follows:

$\begin{pmatrix} x & y & 1\end{pmatrix}\begin{pmatrix} a & b & d\\ b & c & e\\ d & e & f\end{pmatrix}\begin{pmatrix} x\\ y\\ 1\end{pmatrix}=0\quad (\ast).$

We write $B$ for the matrix

$\begin {pmatrix} a & b\\ b & c\end {pmatrix}.$

We now want to transform the system $(\ast)$ in such a way that one can immediately read the type of the described conic section. To do this, we take the liberty of determining the coordinates $x,y$ of the plane by an orientation-preserving Euclidean motion

$\begin {pmatrix} x\\ y\end {pmatrix} \mapsto O\begin {pmatrix} x\\ y\end {pmatrix} + w$

(here $O$ is a real orthogonal matrix with determinant 1 and $w\in\mathbb R^2$ is an arbitrary vector). This rotates and shifts the conic section, but does not change its shape.

First we consider the matrix $B$ . Since it is a symmetrical matrix ( $B=B^\top$ , i.e. $B$ merges into itself when mirrored at the main diagonal), there is — according to a well-known theorem from the Linear algebra — a real orthogonal matrix $O$ such that $O^\top BO$ is a Diagonal matrix is, whose Eigenvalues stand on the main diagonal. By possibly swapping the columns of $O$ we can make it so that $\det(O)=1$ . By transition

$\begin{pmatrix} x\\ y\end{pmatrix}\mapsto O\begin{pmatrix} x\\ y\end{pmatrix}$

we thus obtain a quadratic equation of the form $(\ast)$ where the mixed term $2bxy$ vanishes (since $b=0$ ).

We now consider the following cases:

Case 1: $a\neq 0$ and $c\neq 0$ : Then we can perform quadratic completion for both variables $x$ and $y$ . Thus the terms $2dx$ and $2ey$ disappear. So we get a new equation of the form $ax^2+cy^2+f=0$ . Now we have to distinguish between two cases again:

(a) If $f\neq 0$ holds, we can transform the equation so that it is of the form $ax^2+cy^2=1$ . If $a,c\gt 0$ , then it is an ellipse with the semi-axes $r_1=1/\sqrt{a}$ and $r_2=1/\sqrt{c}$ . If exactly one of the parameters $a$ and $c$ is negative, we can assume by means of permutation that $a\gt 0$ and $c\lt 0$ . Then it is a hyperbola with semi-axes $r_1=1/\sqrt{a}$ and $r_2=1/\sqrt{-c}$ . But if $a,c\lt 0$ is valid, one sees immediately that the described conic section is the empty set.

(b) Now let $f=0$ apply (this corresponds to the case where the intersection plane intersects the double cone at its apex). If $a$ and $c$ have the same sign, it is easy to see that the conic section degenerates to exactly one point (namely $(0,0)$ ). If they have opposite signs, two straight lines of the slope $\pm\sqrt{\lvert a/c\rvert}$ through the origin are created.

Case 2: $ac=0$ : If both parameters disappear, then we have an equation of at most 1st degree. This therefore describes either a straight line, the empty set, or the entire plane. Therefore, we may assume that $a\neq 0$ and $c=0$ (except for interchange). By quadratic addition we can assume that $d=0$ . Now we have to distinguish between two cases again:

(a) If $e\neq 0$ holds, we can shift in the $y$ direction so that we get an equation of the form $ax^2+ey=0$ . This describes a parabola.

(b) If $e=0$ is valid, the $y$ variable does not appear in our equation. We therefore obtain two (possibly identical) straight lines parallel to the $y$ -axis as a degenerate conic section.

This finishes the classification of the 2-dimensional conic sections.

Applications and examples

Conic sections are used in astronomy because the orbits of celestial bodies are approximated conic sections. They are also used in optics — as a rotational ellipsoid for car headlights, as a paraboloid or hyperboloid for reflecting telescopes, etc.

Historical

The mathematician Menaichmos (c. 380–320 BC) studied conic sections at Plato’s Academy using a cone model. He discovered that the so-called Delic problem (“cube doubling“) can be traced back to the determination of the intersection points of two conic sections. In the 3rd century BC, Euclid described the properties of conic sections in four volumes of his Elements (which have not yet been found). The entire knowledge of the mathematicians of antiquity about conic sections was summarised by Appolonios of Perge (c. 262–190 BC) in his eight-volume work “Konika” (German: “Über Kegelschnitte”). The analytical description of the totality of conic sections by equations of the type $(\ast)$ was found by Pierre de Fermat (1607–1665) and René Descartes (1596–1650).

Literature

[1] Koecher, M. u. Krieg, A.: Ebene Geometrie, 3. Auflage, Berlin, 2007.