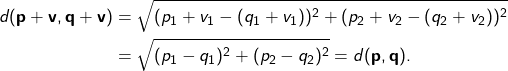Dust circles

The subject of the exhibit “Dust Circles” is an interesting mathematical theorem about plane movements. First of all, you can look at the exhibit: It consists of two transparent plastic plates, each of which has black dust embedded in a congruent manner. The upper of the two is clamped in a wooden frame that can be moved against the lower fixed panel. What can you observe now?

It seems as if circles are involuntarily formed by this displacement — as the name of the exhibit already reveals.

And now the mathematics:

But what is the reason for this phenomenon? For this purpose, we want to introduce a few mathematical terms that enable a precise description of what is observed. To do this, we first introduce the so-called Euclidean metric on the plane $\mathbb R^2$ : Let $\mathbf p=(p_1,p_2)$ and $\mathbf q=(q_1,q_2)$ be two points in the plane. Then their Euclidean distance is defined as

$d(\mathbf p,\mathbf q)\coloneqq\sqrt{(p_1-q_1)^2+(p_2-q_2)^2}.$

A mapping $f\colon\mathbb R^2\to\mathbb R^2$ of the plane in itself that preserves the Euclidean distance, i.e. it is $d(f(\mathbf p),f(\mathbf q))=d(\mathbf p,\mathbf q)$ for all $\mathbf p,\mathbf q\in\mathbb R^2$ , is called isometry. Why do we look at such illustrations? Well, the reasoning lies in the fact that moving the upper plastic disk against the lower one corresponds exactly to such a distance-preserving self-imaging of the plane, because in doing so the distance between two points remains the same, regardless of whether we move the disk.

The question that the exhibit indirectly asks the visitor is this: What distance-preserving self-images of the Euclidean plane exist at all?

We want to fully clarify this question in the course of this short in-depth text. To do this, we first observe that any translation around a given vector $\mathbf v=(v_1,v_2)\in\mathbb R^2$ is distance-preserving, because it holds

$\begin{align*} d(\mathbf p+\mathbf v,\mathbf q+\mathbf v)&=\sqrt{(p_1+v_1-(q_1+v_1))^2+(p_2+v_2-(q_2+v_2))^2} \\ &=\sqrt{(p_1-q_1)^2+(p_2-q_2)^2}=d(\mathbf p,\mathbf q). \end{align*}$

But the translations are now in bijection with the vectors $\mathbf v\in\mathbb R^2$ themselves. So if $f\colon\mathbb R^2\to\mathbb R^2$ is a distance-preserving mapping, we can form the mapping $f'=f-f(\mathbf 0)$ , which still preserves the Euclidean distance but now fixes the zero point $\mathbf 0$ . Therefore, we may assume that $f(\mathbf 0)=\mathbf 0$ . Now let us consider the images of the two standard unit vectors $\mathbf e_1$ and $\mathbf e_2$ under $f$ . The right triangle $\triangle(0,\textbf{e}_1,\textbf{e}_2)$ is determined by the lengths of its sides (namely $1$ , $1$ and $\sqrt{2}$ ) up to congruence. However, these are preserved under $f$ , so that $f(\mathbf e_1)$ and $f(\mathbf e_2)$ must again be unit vectors perpendicular to each other. Consider further that each vector $\mathbf v=(v_1,v_2)\in\mathbb R^2$ is uniquely determined by its distances to the three points $\mathbf 0$ , $\mathbf e_1$ , $\mathbf e_2$ . Namely, these are exactly

$a=\sqrt{v_1^2+v_2^2}, b=\sqrt{(v_1-1)^2+v_2^2}, c=\sqrt{v_1^2+(v_2-1)^2},$

so that $a^2-b^2=2v_1-1$ and $a^2-c^2=2v_2-1$ uniquely define the parameters $v_1$ and $v_2$ . But with this $f(\mathbf v)=v_1f(\mathbf e_1)+v_2f(\mathbf e_2)$ must be, because this vector has the same distances to $\mathbf 0=f(\mathbf 0)$ , $f(\mathbf e_1)$ , $f(\mathbf e_2)$ as $\mathbf v$ to $\mathbf 0,\mathbf e_1,\mathbf e_2$ . Thus, the mapping $f$ must now even be linear (because this corresponds exactly to the observation just made). But since $f$ also maps the orthonormal basis $\mathbf e_1,\mathbf e_2$ to such a basis again, $f$ corresponds to an orthogonal $2\times 2$ matrix. However, these matrices can now be described very simply: To do this, we assume that $\mathbf e_1$ is mapped onto the unit vector $\mathbf f_1=(a,b)$ . Because $a^2+b^2=1$ , we find an angle $\alpha\in[0,2\pi)$ such that $a=\cos(\alpha)$ and $b=\sin(\alpha)$ (since the equation describes exactly the unit circle). The vector $\mathbf e_2$ must now be mapped to a unit vector $\mathbf f_2=(c,d)$ which is perpendicular to $\mathbf f_1$ . But it already follows that $\mathbf f_2=\pm(-b,a)$ , since there are only two such vectors. Thus $\mathbf f_2=(c,d)=(\mp\sin(\alpha),\pm\cos(\alpha))$ holds. So for $f$ we get the matrix

$M=\begin{pmatrix} \cos(\alpha) & -\varepsilon\sin(\alpha)\\ \sin(\alpha) & \varepsilon\cos(\alpha)\end{pmatrix}.$

Here $\varepsilon\in\{\pm1\}$ can be chosen arbitrarily. If $\varepsilon=+1$ , this simply corresponds to a rotation by the angle $\alpha$ . This fact is the issue highlighted by the exhibit. If, on the other hand, $\varepsilon=-1$ , we obtain a reflection on the straight line $g$ that intersects the $x$ axis at an angle of $\alpha/2$ .

Thus, we have fully understood the distance-preserving self-mappings of the Euclidean plane: Any such mapping $f\colon\mathbb R^2\to\mathbb R^2$ is of the form

$f(\mathbf x)=D_{\alpha,\varepsilon}\mathbf x+\mathbf v$

for a rotation or reflection matrix $D_{\alpha,\varepsilon}$ as above and a vector $\mathbf v$ corresponding to the subtracted translation. However, if we start at the identical self-image (where $\varepsilon=+1$ holds) and take it to a certain other distance-preserving image, the parameter $\varepsilon$ cannot make a “jump” (because otherwise the orientation would suddenly reverse and thus the plate would be flipped, which is not allowed in the exhibit). Thus we can restrict ourselves to the case $\varepsilon=+1$ (if $\varepsilon=-1$ , we can show that then $f$ always represents the reflection on a straight line). Now two cases can occur:

Case 1: $f$ has a fixed point $\mathbf x$ . Then

$f(\mathbf x)=\mathbf x=D_{\alpha,1}\mathbf x+\mathbf v$

holds. From this follows $(\mathrm{id}-D_{\alpha,1})\mathbf x=\mathbf v$ . So $f$ is then given by

$f(\mathbf y)= D_{\alpha,1}\mathbf y+\mathbf x-D_{\alpha,1}\mathbf x=D_{\alpha,1}(\mathbf x-\mathbf y)+\mathbf x,$

which is simply the rotation about the point $\mathbf x$ by the angle $\alpha$ .

Case 2: $f$ has no fixed point. Since the equation

$\mathbf x=D_{\alpha,1}\mathbf x+\mathbf v$

is always solvable for $\alpha\neq 0$ (because $\mathrm{id}-D_{\alpha,1}$ is then not singular), consequently $\alpha=0$ must hold. $f$ is then simply a translation.

The two cases 1 and 2 now completely clarify the phenomenon observed on the exhibit: Either one sees large dust circles (case 1) or at least dust straight lines (case 2).

Finally, it should be noted that observed interesting fact for the group of all orientation-preserving ( $\varepsilon=+1$ ) self-mappings of the Euclidean plane lies group-theoretically in the fact that it is a so-called Frobenius group. This is expressed precisely in the fact that the elements that do not fix a point together with the identity form a subgroup (the translations).

Literature:

[1] https://en.wikipedia.org/wiki/3D_rotation_group

[2] https://en.wikipedia.org/wiki/Isometry

[3] https://en.wikipedia.org/wiki/Euclidean_space

[4] https://en.wikipedia.org/wiki/Orthonormal_basis

[5] https://en.wikipedia.org/wiki/Frobenius_group