Euler’s lines

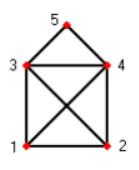
Who doesn’t know the “House of St. Nicholas“? The task is to draw the connecting lines between five points (in the figure 1, 2, 3, 4, 5) “in one go” in such a way that each of these eight lines is traversed exactly once.

One of many possible solutions to this problem is: $1-3-5-4-2-3-4-1-2$ . In the Maths Adventure Land you will find three similar tasks in which the task is to place a string over given lines exactly once around given points. The more points and lines there are, the more difficult it is to find a solution.

And now … the mathematics:

The “House of St. Nicholas” and the three figures shown in the Maths Adventure Land are — formulated mathematically — so-called undirected graphs. An undirected graph consists of a set of points with lines between them. The points are called nodes or corners, the lines are called edges. Such a graph is called connected if every node is connected to every other node by a “path“, i.e. by a sequence of edges bound to each other (to nodes). The “House of St. Nicholas” is such a connected graph. It has five nodes: $1$ , $2$ , $3$ , $4$ , $5$ and eight edges: $1-2$ , $1-3$ , $1-4$ , $2-3$ , $2-4$ , $3-4$ , $3-5$ , $4-5$ .

The simplest model in the ADVENTURE LAND MATHEMATICS also represents a connected graph. It has 6 nodes and 12 edges.

Connected graphs are called Euler lines, “closed” Euler circles or Eulerian paths after the mathematician Leonhard Euler (1707–1783). In mathematics (especially in its subfield of graph theory), it is a cycle that contains all edges of a graph exactly once. A connected graph that has an Eulerian line is also called an Eulerian graph. In 1736, Euler solved the so-called Königsberg bridge problem: the Pregel river flows through the former East Prussian town of Königsberg (since 1945 Russian: Kaliningrad). In Euler’s time, there were seven bridges over this branching river. The question was raised whether there was a circular route where each bridge would be crossed exactly once.

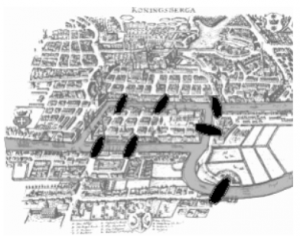
If there is such a circular path, then the proof of its existence is simply to show this path. A serious mathematical problem, on the other hand, is to prove that such a path cannot exist. Leonhard Euler was able to prove in his “Solutio problematis ad geometriam situs pertinentis” that there is no such circular route if there are more than two islands or adjacent areas that can be reached via an odd number of bridges. Euler’s considerations led directly to graph theory as a sub-discipline of modern mathematics.

Literature

[1] Diestel, R.: Graphentheorie, 3. Auflage, Berlin / Heidelberg, 2006.

[2] Fellmann, E. A.: Leonhard Euler, Basel, 2006.

[3] Jungnickel, D.: Graphen, Netzwerke und Algorithmen, 3. Auflage, Darmstadt, 1994.

[4] Velminski, W.: Leonhard Euler. Die Geburt der Graphentheorie, Berlin, 2008.