Galilei’s Tank
As shown in Figure 1 below, the so-called Galilean trough consists of a rectilinear channel inclined by an angle ![]() and having an approximately semicircular cross-section.
and having an approximately semicircular cross-section.
As shown in Figure 1 below, the so-called Galilean trough consists of a rectilinear channel inclined by an angle ![]() and having an approximately semicircular cross-section.
and having an approximately semicircular cross-section.
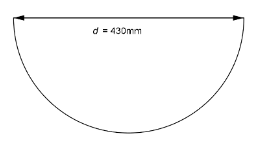
In EXPERIENCE LAND MATHEMATICS, the trough, i.e. the Galilean trough, is a blue tread with a length of ![]() , which is inclined at the angle
, which is inclined at the angle ![]() with respect to the horizontal. The approximately semi-circular cross-section of the channel, which is constant over the entire length, is “bounded upwards” by an “imaginary” straight line. The distance it generates has length
with respect to the horizontal. The approximately semi-circular cross-section of the channel, which is constant over the entire length, is “bounded upwards” by an “imaginary” straight line. The distance it generates has length ![]() as shown in Figure 2 below:
as shown in Figure 2 below:

There are small obstacles in the “bottom” of the Galilei trough so that a ball starting at a right angle (to the trough) and at the top of the right edge (in the direction of travel) of the Galilei trough does not touch it as it travels “down“, if a suitable start of the ball is made. For this, there are 10 different starting possibilities as “small” rectilinear depressions attached perpendicular to the Galilei trough (see figure 2). The experimenter now has the task of finding the launch option that allows the ball to travel downwards “undisturbed“, i.e. without touching the obstacles. The path traversed by the sphere then approximately represents a “distorted” cosine-shaped movement.
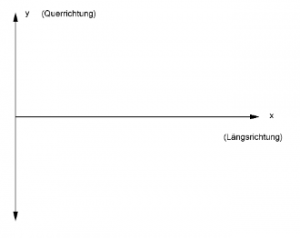
The motion of the sphere is approximately the motion of a point mass on a two-dimensional surface, represented by a Cartesian ![]() coordinate system. The (positive)
coordinate system. The (positive) ![]() -direction describes the direction of the valley bottom running from top to bottom and the (positive)
-direction describes the direction of the valley bottom running from top to bottom and the (positive) ![]() -direction describes the direction running perpendicular to it from the valley bottom to the right (in running direction) upper edge of the Galilei trough (see following figure 3):
-direction describes the direction running perpendicular to it from the valley bottom to the right (in running direction) upper edge of the Galilei trough (see following figure 3):
 and
and 
The motion of the sphere in ![]() -direction is then determined — neglecting friction — by the displacement-time law
-direction is then determined — neglecting friction — by the displacement-time law
![]()
for ![]() (where
(where ![]() denotes the time in seconds). Where
denotes the time in seconds). Where ![]() is the acceleration due to gravity and
is the acceleration due to gravity and ![]() is the angle of inclination of the Galilean trough. In the
is the angle of inclination of the Galilean trough. In the ![]() -direction there is approximately a harmonic oscillation (“cosine oscillation“) of the form
-direction there is approximately a harmonic oscillation (“cosine oscillation“) of the form
![]()
before. Here ![]() denotes the angular frequency of this oscillation and
denotes the angular frequency of this oscillation and ![]() the amplitude with
the amplitude with ![]() .
.
Rearranging the equation ![]() according to time, we get:
according to time, we get:
![Rendered by QuickLaTeX.com \[(1)\Rightarrow t^2=\frac{2x(t)}{g\sin(\alpha)}\Rightarrow t=\sqrt{\frac{2x(t)}{g\sin(\alpha)}}\quad (3).\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-f7e2c1f61cd0d83bb90251ba919485d2_l3.png)
Consequently, for all time points ![]() one obtains the path-time law
one obtains the path-time law ![]() in
in ![]() -direction as a function of the path-time law
-direction as a function of the path-time law ![]() in
in ![]() -direction:
-direction:
![Rendered by QuickLaTeX.com \[(2),\,(3)\Rightarrow y(t)=A\cos\left(\omega\sqrt{\frac{2x(t)}{g\sin(\alpha)}}\right)\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-7918a8f98165ad3a706994c4fda63d38_l3.png)
for ![]() , i.e.
, i.e.
![Rendered by QuickLaTeX.com \[y=A\cos\left(\omega\sqrt{\frac{2x}{g\sin(\alpha)}}\right)\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-759460d1b7ee1ab9f4604ea5b8982eed_l3.png)
and thus
![]()
with ![]() and
and ![]() . So
. So ![]() with the concrete values for the angle of inclination
with the concrete values for the angle of inclination ![]() , the amplitude
, the amplitude ![]() and the angular frequency
and the angular frequency ![]() :
:
![]()
Then the trajectory of the ball rolling “downwards” is approximately described by the curve shown in figure 4:
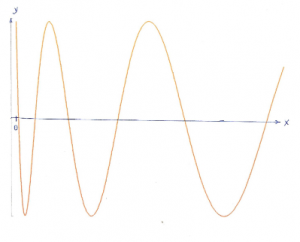
 diagram of the path curve
diagram of the path curve