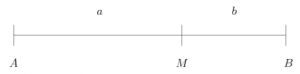Golden Ratio
The Golden Section (Latin: sectio aurea) or also “Divine division” (Latin: proportio divina) consists in the division of a distance ![]() in two sections
in two sections ![]() and
and ![]() , so that the length of the longer section
, so that the length of the longer section ![]() to the length of the shorter section
to the length of the shorter section ![]() behaves like the length of the total distance
behaves like the length of the total distance ![]() to the length of the longer section
to the length of the longer section ![]() (cf. Figure 1):
(cf. Figure 1):