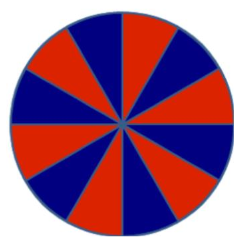
How big is the area of a circle?

This question already preoccupied the Egyptians around 2000 BC. This exhibit should help you find an answer to this question yourself. By “cleverly” flipping sectors of a given circle, one can see that its area is exactly the same as that of a parallelogram-like figure (cf. Figure 3). In this way, one obtains a relationship between the circumference and the area of a circle.

And now … the mathematics:

First, you decompose the given circle into $n$ congruent circle sectors. Here $n$ should be even (for odd $n$ an analogous procedure, but with a “trapezoid” instead of a “parallelogram”, would lead to the same result). In our example $n=12$ was chosen.

Wie groß ist die Fläche eines Kreises v1

Each of these sectors has the following shape:

Wie groß ist die Fläche eines Kreises v2

Anyone who takes a closer look at the exhibit quickly realises that simple “trial and error” or even “brute force” will not get you anywhere with the task of determining the area of the circle, at least approximately. But there is a good approximate solution. This looks like this:

Wie groß ist die Fläche eines Kreises v3

One now looks for correlations between the underlying circle and the associated “parallelogram” (Figure 3). It applies:

The circle and the “parallelogram” have the same area.
As $n$ increases, the “parallelogram” becomes more and more like a rectangle whose height is the radius $r$ of the given circle and whose width is equal to half the circumference $p/2$ of the same.

Why? The reason(s):

Since the circle and the “parallelogram” are composed of the same parts, both must have the same area. Expressed mathematically: equality of decomposition implies equality of content.
The sectors of the circle of the same size come closer and closer to a distance of length $r$ as $n$ grows. In the “parallelogram” they stand “upright“. Therefore, its height approaches more and more the radius $r$ (cf. Figure 3).
If the sectors lie in the circle (cf. Figure 1), the circumference $p$ of the circle corresponds to the product $n\cdot b$ of the number $n$ of sectors (in our example $n=12$ ) with the arc length $b$ of a sector (cf. Figure 2). In the “parallelogram” (figure 3), exactly half of the sectors are positioned so that their tip points upwards and the other half in the opposite direction. This arrangement results in the length of the base side of the “parallelogram” approaching more and more the value $\frac{n}{2}\cdot b=p/2$ .

Summarising these considerations, we get for the area $A$ of the parallelogram (which is equal to the area of the circle):

$A=a\cdot h=\frac{p}{2}\cdot r,$

because — as justified above — for $n\to\infty$ it approaches more and more a rectangle of height $h=r$ and base side of length $a=p/2$ . From this follows the formula for the circular area:

$A=\frac{p r} {2} .$

This result can now be brought together with the one from the exhibit “What is Pi?”. There one learns that

$\pi=\frac{p}{d}=\frac{p}{2r}.$

Here $d=2r$ is the diameter of the given circle. Altogether, the area of the circle of radius $r$ is:

$A=\frac{p r} {2} =\frac{p}{2r}\cdot r^2=\pi r^2,$

which corresponds to the known formula for the circular area.