Leonardo Bridge

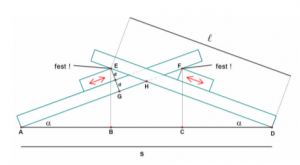
Thanks to the Italian sculptor and art collector at the Spanish court of Philip II, Pompeo Leoni (1533–1608), the artistic and scientific estate of the outstanding Renaissance artist and scientist Leonardo da Vinci (1452–1519), collected in the so-called Codex Atlanticus, has been preserved to this day. This codex, which is kept in the Ambrosian Library in Milan, also contains some drawings with which Leonardo constructed an extraordinary bridge. The “Leonardo Bridge” is composed exclusively of boards, without these being connected by means of dowels, screws, nails, ropes or glue. Of course, the individual boards are shorter than the obstacle to be spanned — a river, for example.

The stability of such a bridge results solely from the position of the individual boards supporting each other. The “instructions for the construction of very light and easily transportable bridges, with which the enemy can be pursued and put to flight” (Leonardo da Vinci, 1483) was not the only invention of the artist who painted the “Mona Lisa“. The universal genius Leonardo also designed, among other things, sluice gates, spinning machines and paddle wheel boats.

And now … the mathematics:

The smallest bridge that can be built according to the principle invented by Leonardo da Vinci consists of eight boards. Each extension requires 4 new boards.

Of course, the question of how large the maximum span of the Leonardo Bridge can be is of particular interest. For the smallest bridge, the following sketch (cf. Hans Humenberger) gives the following results:

The span $s$ can thus be determined in the following way:

$s=\lvert\overline{AD}\rvert=\lvert\overline{AC}\rvert+\lvert\overline{BD}\rvert-\lvert\overline{BC}\rvert.$

So that gives

$s=2\lvert\overline{AC}\rvert-\lvert\overline{EF}\rvert.$

Therefore, $s=2l\cos(\alpha)-2d/\sin(\alpha)$ . Specifically for $l=35\mathrm{dm}$ and $d=1,01\mathrm{dm}$ , this gives the following graphical representation of the function $s=s(\alpha)$ with $\alpha_{\min}\lt\alpha\lt\alpha_{\max}$ in radians:

The maximum value for $s$ in this particular case is found for $\alpha=0.30666\ldots$ in radians, i.e. $\alpha=17.57^\circ$ . In general, the (optimal) value of the angle of rise $\alpha=\alpha_{\mathrm{opt}}$ leading to a maximum range $s$ is a solution of the equation

$d\cos(\alpha)=l\sin^3(\alpha)$

as is easily obtained by derivation.

Literature

[1] Beutelspacher, A. u.a.: Mathematik zum Anfassen, Mathematikum, Gießen, 2005.

[2] Humenberger, H.: Die Leonardo-Brücke. Mathematische und praktische Aktivitätenrund um die Leonardo-Brücke, in: Der Mathematikunterricht 57 (4), S. 34–54, 2011.

[3] Zöllner, F.: Leonardo da Vinci, Kölln, 2006.