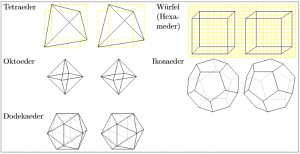
Platonic bodies

Platonic solids (or: ideal solids, regular polyhedra — “polyhedra“) are convex solids with the greatest possible regularity, named after the Greek philosopher Plato (427–347 BC). (Here a body is called convex if with two each of its points $P$ and $Q$ also all points on the connecting line $\overline{PQ}$ belong to it).

This (“greatest possible“) regularity consists in the fact that for each of these solids all side faces are congruent (“congruent”) to each other and that they meet in the same way in each corner.

There are exactly five Platonic bodies:

Specifically, these five bodies have the following properties:

	Side faces	Number of faces	Number of corners	Number of edges	Number of faces in a corner
Tetrahedron	equilateral triangle	4	4	6	3
Cube (Hex- ameter)	squares	6	8	12	3
Octahedron	equilateral triangle	8	6	12	4
Dodecahedron	regular pentagons	12	20	30	3
Icosahedron	equilateral triangles	20	12	30	5

Figure 1: The properties of the five Platonic solids

The Platonic Bodies have played a significant role in intellectual history from ancient Greece through the Middle Ages to our own time. Tetrahedron, hexahedron (cube) and dodecahedron were well known to the students of Pythagoras in the 6th century BC. Theaitetos (4th century BC) was also familiar with octahedron and icosahedron.

Platon has described the solids, which were named after him later, in his work Timaisos detailed and assigned to them the four elements, which were according to the opinion at this time the “World building blocks“, in the following way:

Tetrahedron — Fire;
Hexahedron (cube) — Earth;
Octahedron — Air;
Icosahedron — water.

The later added fifth element “ether” (which was interpreted as “upper heaven” in antiquity and whose existence played a special role in physics until the 19th century) was assigned to the dodecahedron.

Famous is also the attempt of the astronomer Johannes Kepler (1571–1630), in 1596 in his work Mysterium Cosmographicum, to describe the (mean) orbital radii of the six planets known at that time (Mercury, Venus, Earth, Mars, Jupiter, Saturn) by a certain sequence of the five Platonic solids and their inner and outer spheres:

And now … the mathematics:

Already Euclid (about 300 BC) proved in his famous work The Elements that there are exactly five of these Platonic solids.

The following considerations lead to this:

The sum of the interior angles in an $n$ -corner is $(n-1)\cdot180^\circ$ . So every interior angle in a regular $n$ -corner has the value

$\frac{n-2}{n}\cdot 180^\circ.$

(e.g. for an equilateral triangle 60°, for a square 90°, for a regular pentagon 108°, etc.)

If $m$ denotes the number of faces meeting in a corner of the Platonic solid, the sum of their angles must be less than 360°, i.e.

$m\cdot\frac{n-2}{n}\cdot 180^\circ<360^\circ.$

From this now follows $m(n-2)<2n$ , which we further convert to

$(m-2)\cdot(n-2)<4\quad (\ast)$

change over.

Now, since $m>2$ (each of the bounding faces has at least three corners) and $m>2$ (at least three faces meet in each corner of the body), only the following five pairs $(m, n)$ of natural numbers (each greater than 2) satisfy the inequality $(\ast)$ :

$(3,3)$ — tetrahedron;
$(4,3)$ — octahedron;
$(5,3)$ — icosahedron;
$(3,4)$ — cube;
$(3,5)$ — dodecahedron.

This ends the proof.

Literature

[1] Adam, P. and Wyss, A.:Platonic and Archimedean solids, their stellar and polar forms, Stuttgart, 1994.

[2] Beutelspacher, A. u.a.:Mathematik zum Anfassen, Mathematikum, Gießen, 2005.

[3] Euclid: The Elements, Book XIII, ed. u. übs. v. Clemens Thaer, 4. Auflage, Frankfurt am Main, 2003.

[4] Kepler, J.: Mysterium cosmographicum. De stella nova, Hrsg. Max Caspar, München, 1938.

[5] Tiberiu, R.: Reguläre und halbreguläre Polyeder, Berlin, 1987.