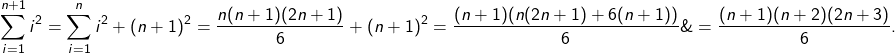Proof without words: Sum of the square numbers
A “proof without words” is so convincing that it is actually taken for a proof, although from the mathematician’s point of view it is not one. However, such a proof is often very suitable for quickly finding a mathematical proof. Why? The presented assumption is not proven universally, but only for some cases, e.g. up to ![]() . A mathematically complete proof would have to cover all possible natural numbers
. A mathematically complete proof would have to cover all possible natural numbers ![]() , i.e. infinitely many cases. This is what one would do for these examples here with the proof principle of complete induction. However, the exhibits are very well suited for making a suitable assumption for a general formula. This is very important, because without a conjecture you also have nothing to prove. Moreover, after careful observation, one can imagine what the next step would look like, then the one after that, and on and on, which is sufficient for a good justification of the facts. Moreover, after careful observation, one can imagine what the next step would look like, then the one after that, and on and on, which is sufficient for a good justification of the facts. Such a proof consists of two parts: the initial step and the inductive step. First, one shows with a simple case (usually
, i.e. infinitely many cases. This is what one would do for these examples here with the proof principle of complete induction. However, the exhibits are very well suited for making a suitable assumption for a general formula. This is very important, because without a conjecture you also have nothing to prove. Moreover, after careful observation, one can imagine what the next step would look like, then the one after that, and on and on, which is sufficient for a good justification of the facts. Moreover, after careful observation, one can imagine what the next step would look like, then the one after that, and on and on, which is sufficient for a good justification of the facts. Such a proof consists of two parts: the initial step and the inductive step. First, one shows with a simple case (usually ![]() ) that the established assumption is correct. This first step is called the initial step. Then, starting from the assumption that the conjecture is correct for an (arbitrary)
) that the established assumption is correct. This first step is called the initial step. Then, starting from the assumption that the conjecture is correct for an (arbitrary) ![]() , it is shown that the conjecture is then also valid for the successor
, it is shown that the conjecture is then also valid for the successor ![]() . This is often illustrated by the image of a ladder on which one has already climbed up to the
. This is often illustrated by the image of a ladder on which one has already climbed up to the ![]() -th step, and from there always gets to the next,
-th step, and from there always gets to the next, ![]() -th step. Like the set of natural numbers, this ladder is also thought to be infinite. The exhibit on the sum of odd numbers consists of
-th step. Like the set of natural numbers, this ladder is also thought to be infinite. The exhibit on the sum of odd numbers consists of ![]() -shaped plastic pieces of different sizes. The first piece consists of one box, the second of 3, the third of 5, etc., the
-shaped plastic pieces of different sizes. The first piece consists of one box, the second of 3, the third of 5, etc., the ![]() th piece of
th piece of ![]() boxes. So if you add up the number of all these boxes, you get the sum of the first
boxes. So if you add up the number of all these boxes, you get the sum of the first ![]() odd numbers. The exhibit even makes it possible for the viewer not to have to do the math himself, but only to add them up. This is because the
odd numbers. The exhibit even makes it possible for the viewer not to have to do the math himself, but only to add them up. This is because the ![]() -shaped parts fit together and, in the correct order (one must not leave any gaps), each results in a square. For each added part (corresponding to another summand when adding), the square grows by one box length in each direction. To be more precise: If you add the part of size
-shaped parts fit together and, in the correct order (one must not leave any gaps), each results in a square. For each added part (corresponding to another summand when adding), the square grows by one box length in each direction. To be more precise: If you add the part of size ![]() , you get a collapsed square with edge length
, you get a collapsed square with edge length ![]() , i.e.
, i.e. ![]() boxes big. This leads to the formula
boxes big. This leads to the formula
![Rendered by QuickLaTeX.com \[1+3+5+\cdots+2n-1=\sum_{i=1}^n{(2n-1)}=n^2.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-4d9ef28d737b271f176c5ab0070b95a0_l3.png)


![Rendered by QuickLaTeX.com \[1+3+5+\cdots+(2n-1)=\sum_{i=1}^n{(2i-1)}=n^2.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-c912fa49ccc26c675194e43feeb1e4f6_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^n{(2i-1)}=1\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-fcb7e6fe97fe7906a02380bae20b3cbc_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^n{(2i-1)}=n^2\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-b95f5f0d718d32f6862e465ad51e3f67_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n+1}{(2i-1)}=(n+1)^2\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-c854d4ce40cb78c68975731adbe3fa63_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n+1}{(2i-1)}=\sum_{i=1}^n{(2i-1)}+(2(n+1)-1)=n^2+2(n+1)-1=n^2+2n+1=(n+1)^2.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-9c8aaa7918edf741de978958af37ce24_l3.png)
![Rendered by QuickLaTeX.com \[1+2+3+\cdots+n=\sum_{i=1}^n{i}=\frac{n(n+1)}{2}.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-20c1077035c631207e60b317c5886471_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^n {i} =1\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-cbe419ee6ec5de0a44d58badebe44a9a_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^n {i} =\frac{n(n+1)} {2} \]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-35e03e6733575f026d5f16df04b9dcd7_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n+1} {i} =\frac{(n+1)(n+2)} {2} \]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-b78099c511c6faa6e44a7bb1f7d7a3ca_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n+1}{i}=\sum_{i=1}^n{i}+(n+1)=\frac{n(n+1)}{2}+n+1=\frac{n(n+1)+2(n+1)}{2}=\frac{(n+2)(n+1)}{2}.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-67a5130e7fb699ae38e7121a773ec9e7_l3.png)

 square numbers
square numbers![Rendered by QuickLaTeX.com \[1^2+2^2+3^2+\cdots+n^2=\sum_{i=1}^n{i^2}=\frac{n(n+1)(2n+1)}{6}.\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-02bcdbdb62193de9ac3fa36c12ec7029_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i = 1}^{n}{i^2} = 1\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-330ee40601031e31647a0e3b65e4c7b4_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^n{i^2}=\frac{n(n+1)(2n+1)} {6} \]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-94c0f11ad3676aa1329079988a434069_l3.png)