Pythagoras to lay
This exhibit is about another illustrative proof of the Pythagorean theorem. The well-known theorem states that the side lengths 
, 
and 
of a right triangle satisfy the equation 
(where and are the two sides enclosing the right angle, — called the cathetes — and is the opposite side — the hypotenuse).
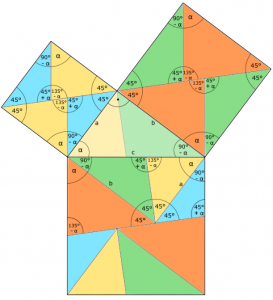
This time the proof is given in the form of a puzzle that the visitor must solve himself in order to comprehend it: Above the catheti are two squares, each divided into four triangles. Each of these triangles is coloured and the two opposite triangles in the square are each congruent (“congruent”) and coloured the same.
If you now cleverly lay the total of eight triangles around, they fill exactly the square above the hypotenuse (see figure 1). This proves the Pythagorean theorem, because equality of content follows from equality of decomposition.
