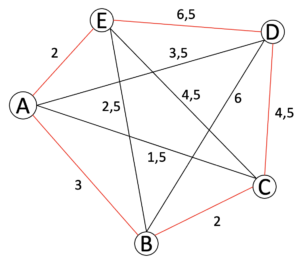
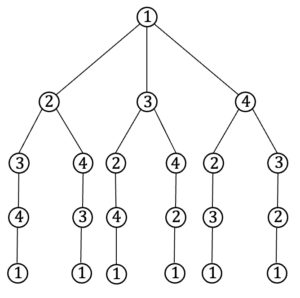
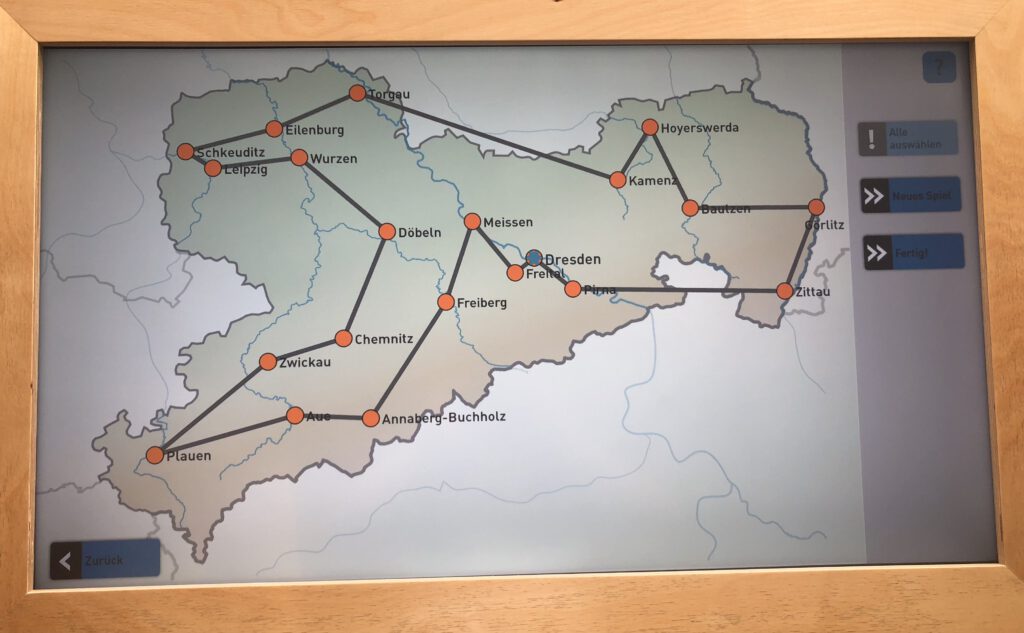
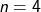Round trips through Saxony
Imagine you are planning a round trip through the largest cities in Saxony. You only want to visit each city once and the round trip should be as short as possible. The “Round trip through Saxony” exhibit allows you to plan your journey as efficiently as possible.