Sound Gyro

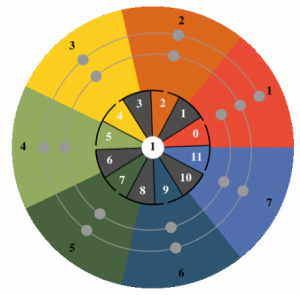
Here you can see the exhibit ” Sound Gyro” in the EXPERIENCE LAND MATHEMATICS. The sound gyro is a musical instrument for one or more players. The playing surface consists of 15 floor sensors arranged along a spiral line on seven coloured circle segments. When the sensors are pressed down with the ball of the foot, sung tone syllables (do, re, mi, fa, so, la, ti) sound in certain pitches. In the centre of the instrument is a rotating cylinder whose 84 positions each encode different distributions of the tone syllables and pitches. The following explanations are intended as an invitation to explore the tonal gyroscope as a medium for the playful communication of both mathematical and music-theoretical insights. Small “compositions” for two, three and more players can be studied here and then tried out on the tonal gyroscope.

Music researchers have gained interesting insights into the structure of the diatonic scale and its modes by mathematical means. These include Eytan Agmon, Gerald Balzano, Norman Carey, John Clough, David Clampitt, Jack Douthett, Julian Hook and Eric Regener. The exhibit is particularly inspired by the following paper: Jack Douthett et al. (2008): Filtered Point-Symmetry and Dynamical Voice-Leading. In: Music Theory and Mathematics: Chords, Collections, and Transformations. University of Rochester Press. This text explains how some of these insights were used in the construction of the sound gyro. The following were involved in the realisation of the exhibit: Thomas Noll (idea and overall concept), Antje Werner and Robert Thiele (design), Firma Kluge (construction), Marije Baalman (sensor technology and programming), Jörg Garbers (programming), as well as the team of the Maths Adventure Land under the direction of Michael Vogt (concept, construction, logistics). The solmisation syllables were sung by students of the Hochschule für Kirchenmusik in Dresden.

First some mathematics: Seven out of twelve

You can divide a circle into seven regular segments and you can divide a circle into twelve regular segments. But you can’t do both at the same time. To be more precise: You cannot select seven corners from a regular dodecagon in such a way that they then form a regular heptagon. After all, the number 7 is not a divisor of the number 12. Even worse: The largest common divisor of 7 and 12 is 1. Nevertheless, there is a maximum regular selection of 7 from 12. It is as regular as possible. What looks like a “lazy compromise” at first glance is the key to an extremely interesting mathematical structure. Figure 2 shows how the maximum regular selection is created. The circle is divided into seven segments on the outside and twelve segments of equal size on the inside.

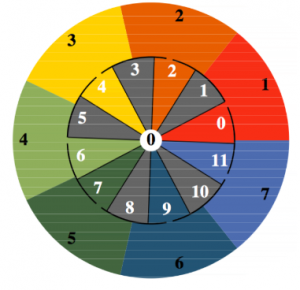
The concrete selection in figure 2 depends on the position of the inner circle imagined as movable in relation to the fixed outer circle. By means of the numbering 1 to 7 (outside) or 0 to 11 (inside), one can identify each segment, while the inner circle turns against the outer one. In the separating black circle line there are exactly seven slits, which are also regularly distributed. They are each located in the middle of the segments of seven. In each configuration, the colour “flows” from the outer and unchanging segments of seven through the slots into the respective passing segments of twelve. This determines the respective selection. There are 84 configurations in total. This can be seen from the counter in the middle (see figure 3 below).

Each of the segments of twelve (white numbers from 0 to 11) moves past the red field of seven (with the black number 1) at some point. Meanwhile, exactly seven configurations result. And: .

The seven steps of the scale

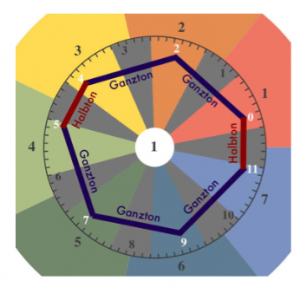
The circular playing surface is divided into seven equally sized coloured segments. These segments embody the seven steps of the diatonic scale.

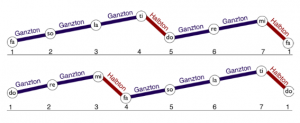
In music theory, the steps are numbered 1, 2, 3, 4, 5, 6, 7. On the playing surface, it is the red field that bears the number 1. From there, the numbers around the circle increase counterclockwise: orange = 2, yellow = 3, etc. (see figure 4 below)

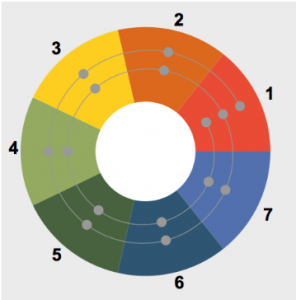
There are ground sensors on each field that trigger sounds when pressed. The sensor positions are connected to each other with a spiral line. This spiral begins and ends on the first level, i.e. the red field with the number 1. Only there are three sensors. All other step fields have two sensors. If you follow the spiral counterclockwise, the pitches of the sounds increase. Both the lowest and the highest note belong to the first step. The notes, each belonging to the same step, are octave-related. To our ears, they sound very similar, although they are far apart in pitch. If you turn the cylinder in the middle of the instrument, the pitches or tone syllables change. Nevertheless, the lowest tone always sounds at the outer end of the spiral and the highest tone at the inner end of the spiral. Step 1 is therefore always the beginning and end of the scale.

The Latin interval designation Octava (i.e. the eighth) is based on the counting of the steps, which here leads exactly once around the circle. The fact that the spiral goes twice around the circle allows a wider range of two octaves for making music.

Seven out of twelve tones

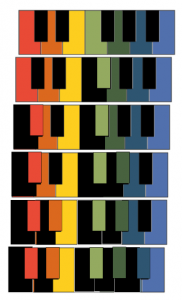
The distribution of the white and black keys on the usual piano keyboard is maximally regular (see figure 5 below, left). Black keys, of which there are only 5, are not adjacent to each other at any point, and the two places where two white keys are adjacent to each other follow each other — as regularly as possible.

The coloured piano keys (see figure 5, right) relate the C major scale C-D-E-F-G-A-H-C’ to the configuration with the number 1 (left). Compared to the piano, the tonal gyroscope has the limitation that only 7 notes per octave register can be played in each individual configuration. So there are no black keys in the strict sense. However, by turning the cylinder, the tone meanings of the coloured step fields can be changed so that those tones that a piano player must produce with black keys become so-called root tones. This means that these tones behave in the same way in the configuration in question as the tones C-D-E-F-G-A-H-C’ in configuration 1.

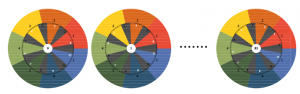
84 diatonic modes

The rotating cylinder in the middle of the sound gyroscope is illuminated from the inside. Seven immobile vertical shadow stripes around the cylinder wall let the light fall only into the seven immobile light stripes in between. The following figure 5 shows an unwinding of the cylinder wall (here still without taking the moving graphic into account).

If one divides the entire cylinder wall all around into 84 equally narrow vertical stripes, 5 of these 1/84 stripes are allotted to each shadow and 7 of these 1/84 stripes are allotted to the areas flooded with light.

This structure is also remotely reminiscent of a piano keyboard. However, at first glance it looks as if there are two too many black keys here. To be more precise: instead of 5 black buttons with the width of 7 narrow stripes each, as one would expect, here there are 7 shadows with the width of 5 narrow stripes each. Figure 9 shows how the already presented method for maximum-regular selection of seven segments out of twelve works with this shadow distribution.

Each of the digits 0, 1, …, 11 is selected exactly and appears accordingly in “white” if it lies within one of the seven coloured segments. Otherwise, it lies in a shadow and appears in “black“. It turns out that none of the digits always appear in two shadows. These shadows therefore remain empty and consequently do not represent black keys. Each selected digit passes through exactly seven adjacent turning positions until it enters a shadow again. These positions can be associated with the tone syllables fa, do, so, re, la, mi, ti. This can be followed in figure 10.

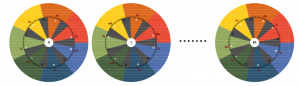
While in each individual position the tone syllables appear in a counterclockwise circle in the order do, re, mi, fa, so, la, ti, the tone syllables associated with a fixed digit pass through the order fa, do, so, re, la, mi, ti from position to position. Why this is so can be seen from a mathematical consideration.

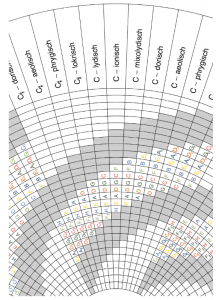
Tones and note names on the cylinder

To designate the twelve chromatic semitones, in traditional music theory, instead of the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, one uses note names, such as C, C#, D, D#, E, F, F#, G, G#, A, A#, H. However, one cannot limit oneself to the selection of these 12 names, because in most of the 84 positions, incorrect namings of the selected tones will then arise. In figure 11, those names that enter one of the seven shadows are replaced by other names before they emerge from the shadow again.

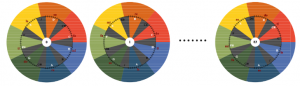
The red level 1 always contains names that begin with the letter C, i.e. …, Cx, C#, C, Cb, … (pronounced: …, Cisis, Cis, C, Ces, …). The orange level 2 always contains names beginning with the letter D, i.e. …, Dx, D#, D, Db, Dbb, … (read: …, Disis, Dis, D, Des, Deses, …), etc. This representation does not yet show the relationship of the note names with different tone letters to each other, as they disappear into the shadows or emerge from there. The structure of the note names is two-dimensional and can be represented in an adequate form on the movable cylinder jacket. Here is an excerpt:

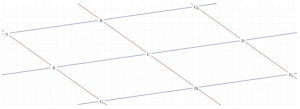
Figure 13 shows how the network of clay names moves against the immobile vertical shadows. The diagonal shadows, which also move along with the vertical, unmoving shadows, have the effect that the seven note names (for the notes just selected), each belonging together in one of the 84 positions, are placed in the illuminated parallelograms, which lie next to each other at the same height all around the cylindrical shell.

Whole tone steps and half tone steps

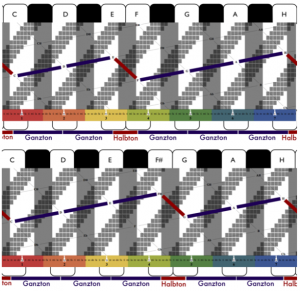
While the seven step segments of the circular playing surface are all the same size, the audible step intervals are of different sizes. There are five larger steps (whole tones) and two smaller ones (half tones). The latter correspond to those two shadows that do not represent black keys.

You can see that the coloured lines for whole tone and half tone intervals (blue and red), are embedded in a whole network of such intervals, which connects all the notes. If you turn the cylinder one position further (see the two graphs placed below each other in Figure 15), exactly two intervals change from the current selection. In the transition from C-ionic (C-D-E-F-G-A-H-C) to C-lydic (C-D-E-F#-G-A-H-C), the semitone E-F is replaced by the whole tone E-F# and, conversely, the whole tone F-G is replaced by the semitone F#-G.

Although here apparently only one spot is “operated on“, the overall step pattern is nevertheless preserved. It is now shifted by four steps. The five intervals between the tone syllables do-re, re-mi, fa-so, so-la and la-ti are always whole tones and the two intervals mi-fa and ti-do are always semitones. As you can see on the left in figure 15, the pattern do-re-mi-fa-so-la-ti reappears shifted by four steps. If you have wondered about this oddity long enough, you can make mathematical considerations for a better understanding.

Tuning gyroscope: Three players form a rotating triangle

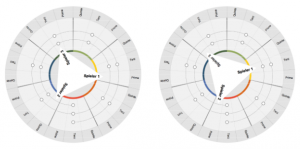
You cannot select three points in a regular heptagon that form a regular triangle, because 3 is not a divisor of 7. However, there is a maximum regular arrangement that forms the basis for a “choreography” for three players here.

Figure 16 below shows the minimum position change of a triangle that turns once in a circle in a total of 21 positions. Its three corners each point to those step fields on which the three players are currently standing and where they should also press down a floor sensor of their choice.

Each time the position of the triangle changes, only one corner crosses the border between two step fields. Consequently, only one player at a time has to take a step further along the spiral. The other two players remain standing with their foot on the sensor that has just been depressed.

The result is a sequence of triads (and their inversions), which in music theory are called diatonic triads. The “mechanics” of the interplay of the three players is based on the same mathematical principle as the selection of the seven diatonic tones from twelve chromatic tones, which underlies the construction of the tonal gyroscope.

Reminder: The movement is counter-clockwise (ascending melody steps) and the person who has two free spaces in front of him/her always takes a step towards the next sensor.

It becomes interesting when both movements are combined: the progression of the three voices in a sequence of triads, as described here, and the alteration of the underlying diatonic modes by turning the cylinder.

Tuning gyroscope: Four players form a rotating square

You cannot select four points in a regular heptagon that form a regular quadrilateral (square), because 4 is not a divisor of 7. However, there is a maximum regular arrangement that forms the basis for a “choreography” for four players here.

Figure 17 shows the minimum change in position of a square that rotates once in a circle in a total of 28 positions. Its four corners point to the level fields on which the four players are currently standing and where they should also press down a floor sensor of their choice.

Each time the position of the square changes, only one corner crosses the border between two step fields. Consequently, only one player at a time has to take a step further along the spiral. The other three players remain standing with their foot on the sensor that has just been depressed.

The result is a sequence of four tones, which in music theory are called diatonic seventh chords. The “mechanics” of the interplay of the four players is thus based on the same mathematical principle as the selection of the seven diatonic tones from twelve chromatic tones, which underlies the construction of the tonal gyroscope.

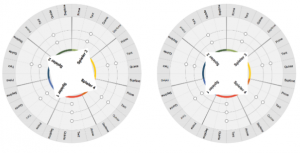
Reminder: Movement is clockwise (descending melody steps) and the player who has another player on the field directly behind them always takes a step towards the next sensor.

It becomes interesting when both movements are combined: the progression of the four voices in a sequence of seventh chords, as described here, and the alteration of the underlying diatonic modes by turning the cylinder.

Some more mathematics: Once again 7 out of 12

If two numbers are divisor-imperfect, i.e. if they have no common divisor except the number 1, then there are multiples of one number that are direct neighbours of certain multiples of the other number. The two number sequences below are the multiples of the divisor-unrelated numbers 7 and 12:

Here 35 and 36 are adjacent ( and ). Similarly, 48 and 49 are adjacent ( and ).

But what does this fact have to do with the sound gyro? We first write the upper (arithmetic) sequence of multiples of 7 each as the sum of a multiple of 12 and a remainder: , , , , , , , . The sequence of the first seven remainders (0, 7, 2, 9, 4, 11, 6) is on the one hand an arithmetic sequence wrapped around the circle (or a regular 12-corner) and on the other hand we already know it as a maximum regular selection of 7 points from a regular 12-corner. So we have two alternative ways of gaining the scale. A curiosity of the numbers 7 and 12? Or a general connection? Is every arithmetic sequence wrapped around a regular polygon maximally regular? We can easily do an experiment with the step size (period) 1. The sequence (0, 1, 2, 3, 4, 5, 6) is undoubtedly an arithmetical sequence, but as corners on the dodecagon (0, 1, …, 11) they all lie next to each other and are anything but regularly distributed. So you have to think a bit about the relationship between the step size and the number of tones. Given the step size 7 and the number 7 of tones involved, 7 times 7 equals . It turns out as follows: It is precisely the above fact that 48 and 49 are neighbours that is responsible for the arithmetic sequence of 7 elements being maximally regular at step size 7. We do not have proof of this claim here. But musicians can realise a third fact that clarifies the proof idea: every diatonic interval (except the prime) comes in two specific sizes: minor and major second, minor and major third, perfect and augmented fourth, diminished and perfect fifth, minor sixth and major sixth, minor and major seventh. These “species” in turn appear in various multiplicities. There are four minor and three major thirds (or three minor and four major sixths). There are two minor and five major seconds (or five minor and two major sevenths). There are six pure fourths and one augmented fourth (or one diminished fourth and six pure fifths). Each decomposition of the total number 7 occurs: , and . From this we can already conclude that the scale must be an arithmetic sequence. Because the decomposition says that there are 6 equal intervals and these must necessarily form a connected chain.

The structure of the scale as an arithmetic sequence is known as the circle of fifths. For a better understanding of the mechanics of altering (turning the cylinder), it is useful to look at this aspect again in more detail. We again take the sequence (0, 7, 2, 9, 4, 11, 6) and add the number 7 to each element and again take the remainder when dividing by 12, obtaining (7, 2, 9, 4, 11, 6, 1). This sequence can be rearranged to (7, 9, 11, 1, 2, 4, 6,) or also to (1, 2, 4, 6, 7, 9, 11) and in both cases also proves to be maximally regular and therefore belongs to other positions of the tone gyroscope. Since we add the number 7, which is also the step size within the sequence, we also get the same remainders if we omit the “0” at the beginning in (0, 7, 2, 9, 4, 11, 6) and add the next element of the arithmetic sequence at the end: the “1”. Although we add 7 to each element, the result differs from the initial sequence only in a single number. After reordering, this is particularly clear: the sequence (0, 2, 4, 6, 7, 9, 11) becomes the sequence (1, 2, 4, 6, 7, 9, 11). In note names: (C, D, E, F#, G, A, H) becomes (C#, D, E, F#, G, A, H). This corresponds to the mode change from C Lydian to C sharp Locrian. Conversely, one can omit the “6” in (0, 7, 2, 9, 4, 11, 6) and instead add the number 5 in front equal to . The sequence (5, 0, 7, 2, 9, 4, 11) is reordered to (0, 2, 4, 5, 7, 9, 11). In note names (C, D, E, F, G, A, H). This corresponds to the mode change from C-Lydian to C-Ionic.

Below, the step patterns of Lydian and Ionic are once again shown in comparison. The shift of the fourth step corresponds either to an exchange of whole tone and semitone in steps 3-4 and 4-5 or to a cyclic permutation of the whole pattern (shift by 4 steps to the right).

In order to appreciate this connection at the descriptive level of step patterns, one can take any seven-letter word as an illustration and conceive of it as a cycle (i.e. after the last letter comes the first again). On the one hand, the letters can be permuted cyclically by so many positions (7 possibilities), on the other hand, two neighbouring letters can be swapped (seven possibilities). For a word like dresden, none of these permutations lead to the same result, although the letters “d” and “e” occur twice.

It is different with the word aabaaab, which represents the step pattern of the Ionic mode. Here the letter “a” stands for whole tone and “b” for semitone. There are seven different cyclic permutations here (see Figure 22). Only four of the seven interchanges of adjacent letters actually yield other words. Two of them, in turn, coincide with cyclic interchanges: aabaaba (mixolydian) and aaabaab (lydian).

Such considerations belong to the field of algebraic combinatorics on words. For further online reading, see [1].

Text: Thomas Noll

Literature

[1] Clampitt, David and Thomas Noll (2010): “Modes, the Height-Width Duality, and Handschin’s Tone Character”, Music Theory Online, Volume 17, Number 1, March 2011.