
As the above Figure 1 shows, the experiment at the exhibit “The Circular Surface“ consists of bending up a circular spring by means of two (initially vertical and parallel) rotatable levers in such a way that its shape in the final position (see Figure 2 below) represents a distance from point ![]() to point
to point ![]() .
.

Here
![]()
is the length of the circumference of the circle that the spring originally formed. Furthermore, the following applies: The area ![]() of the right triangle
of the right triangle ![]() with the vertices
with the vertices ![]() ,
, ![]() and
and ![]() (see Figure 1) is equal to half the area of the circle, i.e.
(see Figure 1) is equal to half the area of the circle, i.e.
![]()
Thus the area ![]() of a circle with radius
of a circle with radius ![]() can be represented by the sum of the areas of two congruent triangles.
can be represented by the sum of the areas of two congruent triangles.
And now … the mathematics:
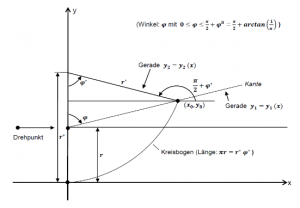
If the two levers are each rotated by the angle ![]() against the vertical axis, the contact point
against the vertical axis, the contact point ![]() between the right lever arm and the bent-up circle results on the right side. The latter now represents itself as a circular arc with the radius
between the right lever arm and the bent-up circle results on the right side. The latter now represents itself as a circular arc with the radius ![]() and the opening angle
and the opening angle ![]() (in radians!). Thus
(in radians!). Thus
![]()
and
![]()
apply.
According to figure 3 above, the following applies to the straight lines ![]() and
and ![]() :
:
![]()
and
![]()
Their intersection ![]() then results as the solution of the equation
then results as the solution of the equation
![]()
i.e.
![]()
and thus
![]()
This results in equation (1):
![]()
and thus
![]()
Equations (1) and (2) then give
![]()
and thus
![]()
which after multiplying out and reducing leads to
![]()
That now means
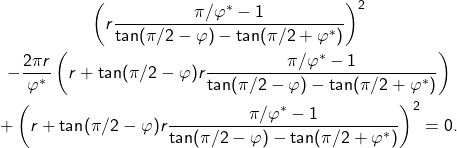
Consequently, it can be assumed without restriction that ![]() , so that for a given opening angle
, so that for a given opening angle ![]() (in radians) of the right lever (see figure 3), the opening angle
(in radians) of the right lever (see figure 3), the opening angle ![]() of the corresponding circular arc (with radius
of the corresponding circular arc (with radius ![]() ) is obtained as the solution of the following equation:
) is obtained as the solution of the following equation:
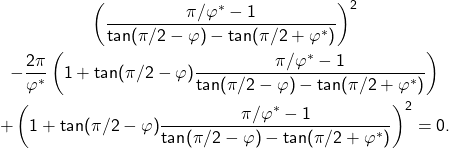
Finally, we give — determined numerically as approximate values — for
![]()
(![]() ) the corresponding angles
) the corresponding angles ![]() and the radii
and the radii ![]() (using the above equation).
(using the above equation).
| | ||||||
|---|---|---|---|---|---|---|
Table 1: The values ![]() and
and ![]() as a function of
as a function of ![]() .
.
Figure 4 below summarises this in a diagram.

 for the different opening angles
for the different opening anglesNote: This exhibit is closely related to the exhibits “What is Pi?”, “What is the area of a circle?” and “Twelve corners”.

