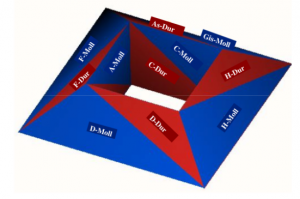
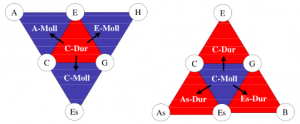
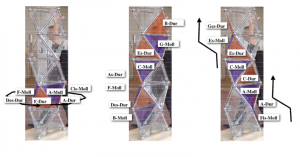
Triad polyhedron

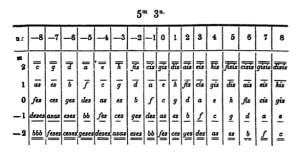
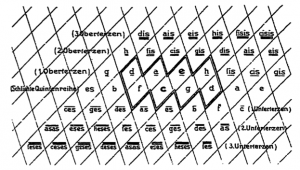
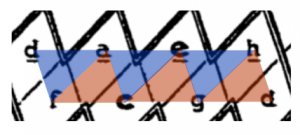
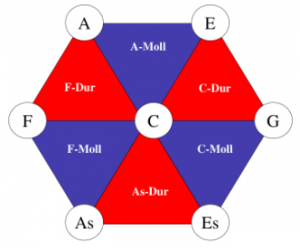
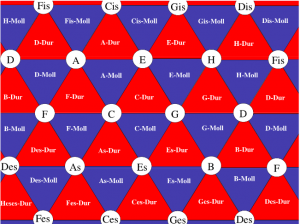
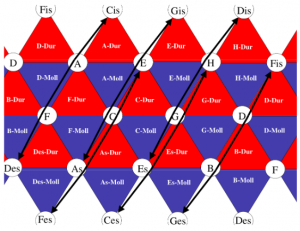
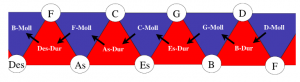
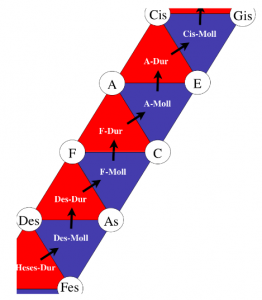
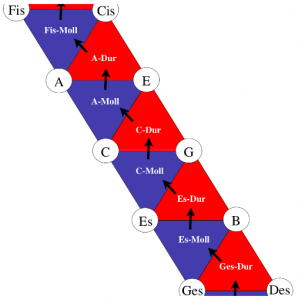
In 19th century music theory, the relationships of tones and triads were studied using two-dimensional representations. The following tone relationship table can be found in Arthur von Oettingen’s treatise “Harmony system in dual development” from 1866. Tones standing next to each other are fifth-related and tones standing on top of each other are major-terz-related. Octave relatedness is neglected in this two-dimensional representation and would be thought of as a third dimension if needed.

The representation in Hugo Riemann (1914) is geometrically a shearing of the above. Here, the large-interz axis points to the upper right and the small-interz axis to the upper left.

Triads are made up of three notes, and can therefore be visualized as triangles. Major triads, such as f-a-c, c-e-g, or g-h-d, form “standing” triangles, and minor triads, such as d-f-a, a-c-e, or e-g-h, form “hanging” triangles. In the following figures, major triads are shown in red and minor triads in blue.

The three notes of a triad have different meanings in relation to it. If you choose any tone, this tone has the meaning of the root tone in a major triad, which is also named after this tone. However, the same note also has the meaning of the third tone in another major triad, as well as that of the fifth tone in yet another major triad. Similarly, he plays these three roles in corresponding minor triads. The figure below shows those 6 triads in which the note C occurs in the mentioned meanings. In the corresponding node of the graph, six triangles collide, the centers of which form the basic cell for a hexagonal honeycomb pattern.

The intervals of the fifth and the major third span a plane that extends infinitely and is completely parceled out by major and minor triads (see the following Figure 5). If one wanted to describe the combinatorics of tone relationships with such a model, then musically this would mean that one would consider the fifth and third relationships to be independent forms of tone relationship.

Combinatorial freedom can be constrained in several ways. In musical notation, for example, fifths and thirds are not independent. Rather, four fifths correspond to a major third (and two octaves). Tones and triads with the same name are then identified with each other.

A further limitation of the repertoire of tones and triads arises when triple major thirds are identified with octaves. One also speaks of enharmonic identification. In the triad polyhedron, which is constructed as a tower of five floors, each of the six horizontal triangles that form the floors’ floors or ceilings corresponds to such a cycle of three major thirds. The concrete pitches sounding there, however, do not result in a cycle of ascending thirds. An interval described here as a major third sounds concretely as a major sixth. The triads also sound in various inversions, which will not be discussed further here.

Strictly limited to 12 tones and 12 major and 12 minor triads each, the result is geometrically a torus covered by 24 triangles. The triad polyhedron with its 30 triangles is a tower whose top floor is enharmonic and octave-equivalent to the bottom floor. It is not closed into a ring.

Apart from the combinatorial overview that can be obtained with the help of these representations, the question arises as to their usefulness for musical analysis. Are there typical triad sequences in pieces of music to which special paths on the triad polyhedron correspond from a geometrical point of view?

The question here is for particularly “economical” triadic sequences, in which only one note in a voice is changed in each step and in which a new triad is nevertheless created. For this purpose, there are always three possibilities from each triad:

They are called changes of fifths (e.g. C major — C minor), changes of thirds (e.g. C major — A minor), and changes of leading tones (e.g. C major — E minor). It is an amazing property of major and minor triads that these triadic connections correspond with the smallest changes in pitch (down to octaves).

Among the many possible triadic paths that can be obtained from the succession of fifth changes, third changes, and leading tone changes, those in which only two of these connection types alternate with each other are of particular interest. These correspond to three different directions on the triad polyhedron. All three appear sporadically in 19th century music.

1. change of thirds and leading tone

This triadic progression reaches all 24 (enharmonically identified) major and minor triads. In the 2nd movement of Ludwig van Beethoven’s 9th Symphony, there is a passage (measures 143–176) where 19 triads are actually passed through.

2. change of fifth and leading tone

This triadic progression reaches exactly 6 of the 24 enharmonically identified major and minor triads. These also consist of a total of 6 tones, which is why one also speaks of the hexatonic cycle here. The piano piece Consolations 3 by Franz Liszt runs through (with the exception of one chord) the hexatonic D flat major cycle. Here, the triads represent tonal regions touched upon in this piece: D flat major, F minor, F major, A minor, A major, (D flat minor is skipped), D flat major.

3. change of fifth and change of third

This triadic progression reaches exactly 8 of the 24 enharmonically identified major and minor triads. These also consist of a total of 8 tones, which is why this is also referred to as the octatonic cycle. The Overture to Rosamunde (Andante measures 1–48) Op. 26 / No. 1 by Franz Schubert runs through such a cycle: C minor, E-flat major, E-flat minor, G-flat major, F-sharp minor, A major, A minor, C major. Again, the 8 triads represent tonal regions touched upon in this piece.

Figure 11 below shows the progression of all three triadic progressions on the triadic polyhedron.