The Coriolis Fountain
The Coriolis fountain is an experiment that can be used to demonstrate the effect of a special form of inertial force called the Coriolis force. It is also sometimes referred to as an illusory force.
The Coriolis fountain is an experiment that can be used to demonstrate the effect of a special form of inertial force called the Coriolis force. It is also sometimes referred to as an illusory force.

This Coriolis force acts on any body whose motion is observed from a rotating reference frame. It was first described mathematically in 1835 by the French mathematician Gaspard Gustave de Coriolis. The Coriolis fountain in the ERLEBNISLAND MATHEMATIK was given its name because the Coriolis effect can be made visible by means of suitably generated water jets. When the Coriolis fountain is rotated, the following phenomena are observed: the water jets emerging from the nozzles located in the center (in the direction of the rim) seem to “bend” against the direction of the rotational movement. And the water jets emerging from the nozzles located at the edge seem to “bend” in the direction of the rotary motion. Both effects increase with greater angular velocity of the disk, i.e. the faster it is rotated by an experimenter. If the water jets of the nozzles from the center meet those from the edge, at that moment the jets are illuminated with blue light. This phenomenon of “bending” water jets can be explained by means of the following mental experiment: Imagine that the nozzles do not emit a continuous water jet, but eject small balls (or individual water droplets) in “rapid” succession. Let the speed of the balls be that of the water jet. The paths of the spheres lined up in the mind can be understood as discretizations of the water jets emerging from the nozzles. Consequently, it is sufficient to analyze the trajectory of a single sphere.
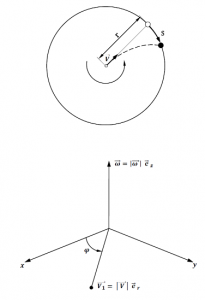
Suppose a circular disk rotates with constant (vector) angular velocity ![]() , which — as a vector — is perpendicular to the plane of rotation. Now, if a sphere with constant (vectorial) velocity
, which — as a vector — is perpendicular to the plane of rotation. Now, if a sphere with constant (vectorial) velocity ![]() is ejected from the center of the spinning disk, then using a system in cylindrical coordinates
is ejected from the center of the spinning disk, then using a system in cylindrical coordinates ![]() and the associated unit vectors
and the associated unit vectors ![]() , we obtain (see Figure 2 below)
, we obtain (see Figure 2 below)
for the Coriolis force, the following formula:
![]()
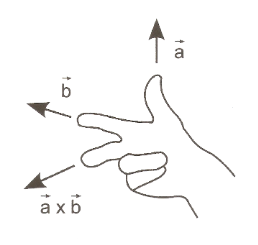
Here ![]() denotes the mass of the sphere and for the determination of the direction of the so-called cross or vector product
denotes the mass of the sphere and for the determination of the direction of the so-called cross or vector product ![]() of two vectors
of two vectors ![]() and
and ![]() the three finger rule applies on the right hand (cf. figure 3 below):
the three finger rule applies on the right hand (cf. figure 3 below):
We will derive this in the following: So where does the above equation for the Coriolis force come from? Let us assume that we, as observers, stand in the center of the counterclockwise rotating disk and follow the sphere that has just been ejected from there in a radial direction. Without rotation (and thus Coriolis force), this would simply strive straight outward (i.e. it moves in time ![]() by the distance
by the distance ![]() along the radius). Now, however, after the ball has been ejected, the disc continues to rotate “to the left” under it (and does not influence it any more). For the rotating observer, this gives the impression that the sphere is striving “to the right” (namely in time
along the radius). Now, however, after the ball has been ejected, the disc continues to rotate “to the left” under it (and does not influence it any more). For the rotating observer, this gives the impression that the sphere is striving “to the right” (namely in time ![]() by the distance
by the distance ![]() ; cf. figure 2 above). This corresponds exactly to a uniformly accelerated motion to the right, with the constant Coriolis acceleration
; cf. figure 2 above). This corresponds exactly to a uniformly accelerated motion to the right, with the constant Coriolis acceleration ![]() . Therefore, it appears to the observer that a force
. Therefore, it appears to the observer that a force ![]() is acting on said sphere according to the above formula.
is acting on said sphere according to the above formula.
1. All movements on the earth are exposed to the Coriolis force (along the equator minimal!), because the earth turns around its own axis and thus represents a rotating reference system. However, the Coriolis force (due to the relatively low approximate angular velocity of the Earth of 360°/24h) only plays a role where large-scale motions occur. Thus, rivers in the northern hemisphere undermine more the right bank, in the southern hemisphere more the left bank (in the direction of flow).
2. The Coriolis force is “responsible” for the fact that air masses around large-scale high-pressure areas in the northern hemisphere of the earth move clockwise, but low-pressure areas move counterclockwise. Thus, in a low pressure area, the air moves inward because of the pressure gradient. This current is deflected to the right in the northern hemisphere by the Coriolis force. This results in a counterclockwise rotary motion.
3. In Foucault’s pendulum (observable as an exhibit in MATHS ADVENTURE LAND), the Coriolis force plays an essential role. The oscillation plane of the pendulum only appears to move. In fact, it maintains its direction while you “circle” the pendulum on the globe.
4. In rail traffic, the Coriolis force in the northern hemisphere causes the rail on the right in the direction of travel to be loaded slightly more than the rail on the left in the case of straight lines. A train (e.g. an ICE 3 with a mass of 400t) traveling at a speed of 250km/h at a latitude of 51° north (e.g. Cologne) experiences a force of 3,200N (Newton) to the right. This corresponds to approx. 0.1% of the weight force. For example, if the train has eight cars with four axles each, each right wheel is pressed against the rail with a Coriolis force of about 100N (Newton) to the right. In comparison, at this speed, a curve radius of 3,000m results in a lateral force of 20,000N on each wheel, i.e. 200 times the value compared to the Coriolis force.
[1] Körner, W.: Physik — Fundament der Technik, 10. Auflage, Leipzig, 1989.
[2] Lindner, H.: Lehrbuch der Physik, 12. Auflage, Leipzig, 1989.
[3] Stommel, H.M. und Moore, D.W.: An introduction to the Coriolis force, New York, 1989.