Flipper
Binärzahlen und das Prinzip der ![]() –
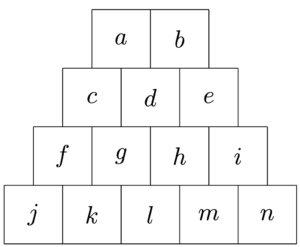
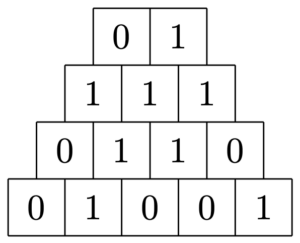
–![]() -Dualität sind aus der Welt der Informatik nicht mehr wegzudenken. Auch das Exponat „Flipper“ verkörpert dieses Prinzip der Dualität. Es besteht aus insgesamt vierzehn Weichen, die sich pyramidenförmig auf vier Ebenen mit jeweils 2, 3, 4 und 5 Weichen verteilen, wie in Abbildung 1 zu erkennen.
-Dualität sind aus der Welt der Informatik nicht mehr wegzudenken. Auch das Exponat „Flipper“ verkörpert dieses Prinzip der Dualität. Es besteht aus insgesamt vierzehn Weichen, die sich pyramidenförmig auf vier Ebenen mit jeweils 2, 3, 4 und 5 Weichen verteilen, wie in Abbildung 1 zu erkennen.

(1) ![]()
Und nun … die Mathematik dazu:
(1) Bei einer Serie von Einwürfen der Kugel kommt es nicht auf deren Reihenfolge an. Wirfst du z.B. die Kugel erst links und dann rechts ein, dann ergibt dies denselben Zustand als wenn du die Kugel erst rechts und dann links eingeworfen hättest.
(2) Wirfst du die Kugel auf einer Seite 16 mal ein (also alle links oder alle rechts), dann landest du beim selben Zustand wie vorher. Andersherum, falls du von einem beliebigen Zustand aus links ![]() -mal und rechts
-mal und rechts ![]() -mal die Kugel einwirfst und der Anfangszustand herauskommt, dann sind sowohl
-mal die Kugel einwirfst und der Anfangszustand herauskommt, dann sind sowohl ![]() als auch
als auch ![]() durch
durch ![]() teilbar.
teilbar.
 bis
bis 
Des Weiteren bezeichnen wir mit ![]() die Operation „Kugeleinwurf links“ und mit
die Operation „Kugeleinwurf links“ und mit ![]() die Operation „Kugeleinwurf rechts“. Beachte, dass der Zustand der linken Dachhälfte}, also der Weichen
die Operation „Kugeleinwurf rechts“. Beachte, dass der Zustand der linken Dachhälfte}, also der Weichen ![]() , nur mittels
, nur mittels ![]() , und die der rechten „Dachhälfte“, also der Weichen
, und die der rechten „Dachhälfte“, also der Weichen ![]() , nur mittels
, nur mittels ![]() geändert werden können. Falls sich die Weichen
geändert werden können. Falls sich die Weichen ![]() und
und ![]() dann jeweils im Zustand 0 befinden, duchlaufen deren Zustände durch Anwendung von
dann jeweils im Zustand 0 befinden, duchlaufen deren Zustände durch Anwendung von ![]() die Binärzahlen von 0 bis 15, wie in Abbildung 3 dargestellt.
die Binärzahlen von 0 bis 15, wie in Abbildung 3 dargestellt.
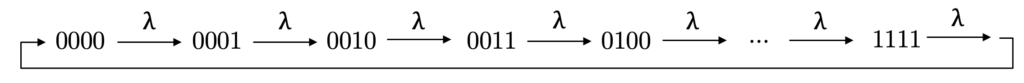
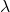
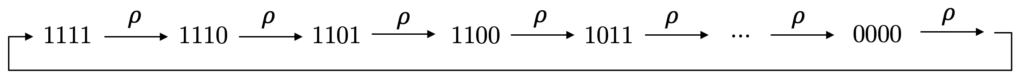
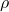
Permutationsgruppen
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
