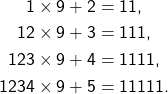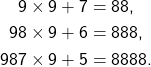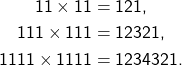Knobeltische

An den Knobeltischen im Ausstellungsraum herrscht oft reges Treiben. Kinder und Erwachsene sitzen nebeneinander, drehen bunte Holzteile in den Händen, rücken Puzzlestücke hin und her, setzen und verwerfen wieder. Mal soll aus sieben Teilen ein Quadrat entstehen — Tangram. Mal gilt es, aus merkwürdig geformten Holzfiguren einen Würfel zu bauen — Soma-Würfel. Oder die Aufgabe lautet, ein Kreuz und ein Quadrat aus denselben Teilen zu legen — das Quadrakreuz.

Wer so knobelt, kennt das Gefühl: Erst scheint es unmöglich, dann taucht plötzlich eine neue Idee auf, und mit einem Mal passt alles zusammen. Das Aha-Erlebnis ist da.

Aber was hat das mit Mathematik zu tun? Eine ganze Menge. Denn alle diese Knobeleien beruhen auf Strukturen, Symmetrien und logischen Mustern. Sie sind sozusagen Mathematik zum Anfassen.

Genau an dieser Stelle schließt die Wandgestaltung in unserem Knobelbereich an. Während auf den Tischen geometrische Figuren gepuzzelt werden, findet sich an der Wand das Pendant in der Welt der Zahlen. Auch hier sind es Puzzles — nur eben in Form von überraschenden Rechnungen.

Zahlen, die sich zu langen Reihen von Einsen aufbauen. Ziffernfolgen, die beim Quadrieren eine kleine Pyramide ergeben. Rückwärts gezählte Zahlen, die in lauter Achten münden. Auf den ersten Blick wirken sie wie kleine Taschenspielertricks, fast zu schön, um wahr zu sein. Aber in Wahrheit steckt auch hier nichts anderes dahinter als Mathematik — dieselbe Ordnung, die auch die Puzzle-Teile so faszinierend macht.

Und nun … die Mathematik

Die magische Neun

Schauen wir uns zunächst die wohl ein der bekannteste Reihen an:

$12345679 \times 9 = 111111111 .$

Die Zahl $12345679$ wirkt zunächst unscheinbar, fast wie die Ziffernreihe $123456789$ — nur ohne die Acht. Doch multipliziert man sie mit 9, verwandelt sie sich in neun Einsen. Und das geht weiter:

$\begin{align*} 12345679 \times 18 &= 222222222, \\ 12345679 \times 27 &= 333333333, \\ & \ \ \vdots \\ 12345679 \times 81 &= 999999999. \end{align*}$

Allgemein gilt:

$12345679 \times (9 \cdot n) = \underbrace{nnnnnnnnn}_{9\ \text{mal}} .$

Aber warum ist das so? Das liegt daran, dass die Zahl $12345679$ nichts anderes ist als

$12345679 = \frac{111111111}{9}.$

Die Zahl $111111111$ besteht aus neun Einsen. Multiplizieren wir mit $9n$ , so „ersetzt“ dieses $n$ jede der neun Einsen durch dieselbe Ziffer $n$ . Dadurch entstehen genau die gleichförmigen Zahlenfolgen.

Die Pyramiden der Einsen

Eine andere, nicht weniger verblüffende Reihe ist diese:

$\begin{align*} 1 \times 9 + 2 &= 11, \\ 12 \times 9 + 3 &= 111, \\ 123 \times 9 + 4 &= 1111, \\ 1234 \times 9 + 5 &= 11111. \end{align*}$

Links wächst die Zahl Ziffer für Ziffer an. Multipliziert mit 9 und anschließend um eine kleine Zahl ergänzt, entsteht rechts eine „Zahlenpyramide“ aus lauter Einsen.

Warum funktioniert das? Die Struktur steckt im Dezimalsystem selbst. Nehmen wir als Beispiel:

$1234 \times 9 = 11106.$

Addiert man nun $5$ , so ergibt sich

$11106 + 5 = 11111.$

Der kleine „Korrekturwert“ gleicht also den Rest so aus, dass eine perfekte Folge von Einsen entsteht. Für jede weitere Stufe gibt es genau die passende Zahl, die hinten ergänzt werden muss.

Die Achten von oben

Ein spiegelbildliches Muster entsteht mit den rückwärts gezählten Ziffern:

$\begin{align*} 9 \times 9 + 7 &= 88, \\ 98 \times 9 + 6 &= 888, \\ 987 \times 9 + 5 &= 8888. \end{align*}$

Auch hier wächst die linke Seite nach und nach, diesmal jedoch absteigend: 9, 98, 987, 9876 \dots Rechts erscheinen ganze Reihen von Achten.

Warum funktioniert das? Das Dezimalsystem sorgt auch hier für die Symmetrie. Zum Beispiel:

$987 \times 9 = 8883.$

Addiert man $5$ , ergibt sich

$8883 + 5 = 8888.$

Die ergänzende Zahl gleicht wieder genau den Übertrag aus, sodass am Ende eine Kette aus Achten steht.

Quadratzahlen mit Symmetrie

Und dann gibt es noch die sogenannten „Repunit“-Zahlen — Zahlen, die nur aus Einsen bestehen:

$1, \quad 11, \quad 111, \quad 1111, \dots$

Ihre Quadrate ergeben wunderschön symmetrische Zahlenpyramiden:

$\begin{align*} 11 \times 11 &= 121, \\ 111 \times 111 &= 12321, \\ 1111 \times 1111 &= 1234321. \end{align*}$

Warum funktioniert das? Die Repunit-Zahlen haben die Form

$R_n = \frac{10^n - 1}{9}.$

Quadriert man $R_n$ , erhält man eine Zahl, deren Ziffernfolge von 1 bis $n$ ansteigt und sich dann wieder zurückspiegelt. Das liegt daran, dass die Entwicklung von $(10^n - 1)^2$ in einer arithmetischen Reihe von Summanden mündet, die genau dieses symmetrische Muster erzeugt.

Fazit

Ob Soma-Würfel, Tangram oder Slothouber-Graatsma-Würfel — bei all den Knobelpuzzles im Ausstellungsraum geht es um Muster, Symmetrien und unerwartete Lösungen. Ganz ähnlich verhält es sich mit den Zahlenrätseln an der Wand.

Sie sind kleine mathematische Kunstwerke, die auf den ersten Blick wie Zaubertricks wirken, bei genauerem Hinsehen aber klare Strukturen offenbaren. Die Einsen-Reihen, die Achten-Spiegelungen und die Repunit-Quadrate sind nichts anderes als Zahlenpuzzles.

So treffen sich zwei Welten: die greifbare der Holz- und Kartonpuzzles auf den Tischen und die abstrakte der Zahlen an der Wand. In beiden steckt dieselbe Freude: Aus scheinbar wirrem Material — ob Figuren oder Ziffern — entsteht plötzlich eine überraschende, elegante Ordnung.

Das ist es, was Mathematik ausmacht: Sie macht das Unsichtbare sichtbar und lässt uns staunen über die Schönheit, die in den einfachsten Mustern verborgen liegt.