Pythagorean theorem

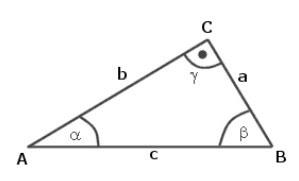
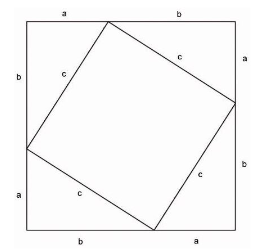
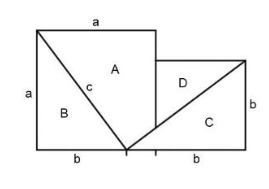
The Pythagorean theorem is one of the fundamental theorems of two-dimensional geometry. It states that for all right-angled triangles (cf. Figure 1) the side lengths are in a certain ratio to each other: If one forms a square over each of the three sides, the sum of the areas of the two smaller squares (over the Cathetes $a$ and $b$ ) is exactly as large as the area of the large square (above the hypotenuse $c$ ). Expressed as an equation, the Pythagorean theorem is therefore simply $a^2+b^2=c^2$ .

Pythagoras himself was born around 570 BC on the Greek island of Samos, the son of a goldsmith. After familiarising himself with the knowledge of the time, especially Babylonian and Egyptian science, by studying with learned priests and travelling, Pythagoras founded his own school with which he wanted to lead his students to “inner purity“. Pythagoras prescribed mathematica for his pupils and had them concentrate on arithmetic, geometry and musicology.

The knowledge of the aspect ratios on a right-angled triangle was already known to Babylonian scholars around 1800 BC and also in India by the 6th century BC at the latest. The role Pythagoras played in teaching the theorem later named after him and in his mathematical proof is not without controversy (see Figure 2).

And now … the mathematics:

Today we know a multitude of proofs for the Pythagorean theorem. One of these is based on the following consideration (see figures 3a and 3b):

The outer square in Figure 3a has the side lengths $a+b$ and thus the area $A=(a+b)^2$ . However, this area is also obtained by adding the areas $A_1=4\cdot\frac{ab}{2}$ of the four right-angled triangles with the cathetus lengths $a$ and $b$ and the area $A_2=c^2$ of the twisted square of side length $c$ inscribed in the large square (cf. Figure 3b). So now

$A=(a+b)^2=a^2+2ab+b^2=4A_1+A_2=2ab+c^2,$

from which the desired identity $a^2+b^2=c^2$ follows by subtracting $2ab$ on both sides.

The exhibit in the Maths Adventure Land shows the correctness of Pythagoras’ theorem in a (different) elementary way (see figures 4a and 4b below):

By folding the surface $B$ (to the left) and the surface $C$ (to the right) around the pivot points $(I)$ and $(II)$ , respectively, up to the stop (cf. Figure 4a), one obtains from a square with the side length $c$ (i.e. the surface area $c^2$ ) two squares lying next to each other with the surface areas $a^2$ and $b^2$ (cf. Figure 4b).

Finally, something literary

We conclude with a — mathematically not to be taken entirely seriously — literary treatment. The German poet Adalbert von Chamisso (1781–1838) describes the legendary sacrifice Pythagoras is said to have made to the gods after discovering “his” theorem:

Of the Pythagorean theorem

The truth, it exists for eternity,

Once the stupid world has seen its light;

The theorem named after Pythagoras

Applies today as it did in its time.

A sacrifice consecrated Pythagoras

To the gods who sent the ray of light to him;

It announced, slaughtered and burned,

One hundred oxen his gratitude.

The oxen since the day when they smell,

That a new truth may be revealed,

Raise an inhuman roar;

Pythagoras fills them with horror;

And powerless to resist the light

They close their eyes and tremble.

(quoted from Project Gutenberg, All the Poems of Adelbert von Chamisso)

Literature

[1] Dewdney, A.K.: Reise in das Innere der Mathematik, Berlin, 2000.

[2] Fraedrich, A.M.: Die Satzgruppen des Pythagoras, Mannheim, 1995.

[3] Maor, E.: The Pythagorean Theorem: A 4,000-year History, Princeton, 2007.

[4] Schupp, H.: Elementargeometrie, Stuttgart, 1977.

[5] Singh, S.: Fermats letzter Satz, München, 2000.

[6] v. Wedemeyer, I.: Pythagoras, Weisheitslehrer des Abendlandes, Ahlerstedt, 1988.