
As this picture of a sliced poultry sausage shows — and as we see it every day “at the butcher’s” — sausages are very often cut at an angle. Geometry teaches us that the intersection is then not bounded by a circle but by an ellipse. If one cuts the sausage shell parallel to the “main axis” of the sausage and places it on a flat surface, the initially “spatial cut” becomes a flat curve that represents part of a so-called sine curve, i.e. a harmonic oscillation.
The associated exhibit in the Maths Adventure Land (see Figure 2 below) shows how a hand crank is used to map the plane, oblique section of a straight (circular) cylinder onto an endless sheet. The image on the slide turns out to be a harmonic oscillation. It is mathematically described by an angular function (on the right-angled) triangle, the so-called sine.

And now … the mathematics:
1. definition of the sine function
According to the following figure 3, the sine (also: sine function) ![]() of an angle
of an angle ![]() is the length of the so-called opposite cathetus in a right triangle with a hypotenuse of length one.
is the length of the so-called opposite cathetus in a right triangle with a hypotenuse of length one.
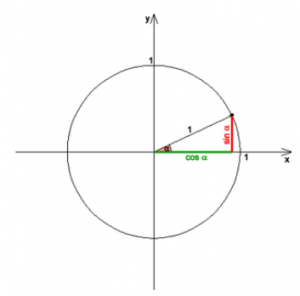
By means of a unit circle (radius ![]() ) one assigns to each angle
) one assigns to each angle ![]() the length of the arc
the length of the arc ![]() over this angle
over this angle ![]() . Considering that the circumference of the unit circle is equal to
. Considering that the circumference of the unit circle is equal to ![]() , the corresponding radian is
, the corresponding radian is ![]() :
:
Table 1: Relationship between degrees and radians
The sine function ![]() is defined by
is defined by ![]() . The length of the so-called adjacent cathetus in a right triangle with a hypotenuse of length 1 over the angle
. The length of the so-called adjacent cathetus in a right triangle with a hypotenuse of length 1 over the angle ![]() with the arc length
with the arc length ![]() is called the cosine (also: cosine function)
is called the cosine (also: cosine function) ![]() with
with ![]() .
.
2. unwinding of the plane cut
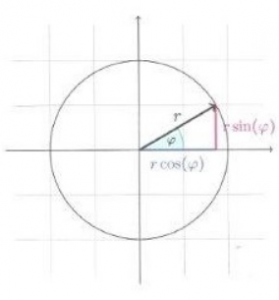
A (straight) circular cylinder with radius ![]() for the base circle (in the ADVENTURELAND MATHEMATICS
for the base circle (in the ADVENTURELAND MATHEMATICS ![]() ) is described by the following equations because of the equation
) is described by the following equations because of the equation ![]() (Pythagorean theorem on the unit circle):
(Pythagorean theorem on the unit circle):
![Rendered by QuickLaTeX.com \[\begin {pmatrix} x(\varphi)\\ y(\varphi)\\ z(\varphi)\end {pmatrix} =\begin {pmatrix} r\cos(\varphi)\\ r\sin(\varphi)\\ z\end {pmatrix} \quad(1).\]](https://erlebnisland-mathematik.de/wp-content/ql-cache/quicklatex.com-75e2b6c5465dfee948ead33da695ebdf_l3.png)
Here ![]() and
and ![]() are the so-called polar coordinates, as shown in the following figure 4:
are the so-called polar coordinates, as shown in the following figure 4:
A plane section of the circular cylinder (at the angle of ![]() ) is given by the bisector in the
) is given by the bisector in the ![]() -plane
-plane
![]()
From equations (1) and (2) thus follows
![]()
for ![]() . This sine function is visible with
. This sine function is visible with ![]() on the slide to be unrolled at the corresponding exhibit in the ADVENTURELAND MATHEMATICS.
on the slide to be unrolled at the corresponding exhibit in the ADVENTURELAND MATHEMATICS.

