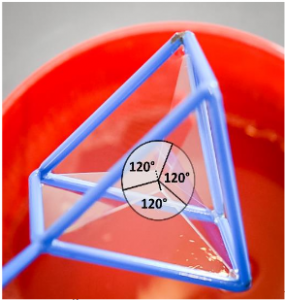
Wonderful Soap Films
I wonder if you can also create “angular soap bubbles“? Of course! By dipping various edge models in soapy water, the most diverse, fascinating shapes are created. So it even proves to be quite difficult to wet the surface of a cube with soap skin. More often, a much more delicate-looking structure is created with a small square or even cube in the centre, to which soap skins stretch from the edges of the cube: