Tracery

In a small town in the Bergisches Land region stands one of the most important Gothic church buildings in Germany.

Construction of Altenberg Cathedral began in 1259 and was completed around 1400. The famous west window of the church is considered the largest Gothic tracery window “north of the Alps“. Designed by an anonymous artist called the “Master of the Berwordt Retable“, the stained glass of the window reflects the medieval idea of the “Holy Jerusalem“, as the place of Christian end-time expectations. Altenberg Cathedral, built as a monastery church, served as a burial place for the dukes and counts of Berg and Jülich-Berg until 1511 and is now the joint parish church for both the Protestant and Catholic communities of the town.

A tracery or tracery window — as shown in the exhibit (as a spatial puzzle) in ADVENTURE LAND MATHEMATICS (cf. figures 2 and 3 below) — is understood to be a geometrically constructed ornamental form of the Gothic period.

The filigree architecture of the arches, points and circles formerly made and joined by stonemasons was initially used to design large windows, especially on sacred buildings. Later, so-called blind tracery was also used to structure wall surfaces and gables, and openwork tracery was used for parapets. In the late Gothic period, the tracery became increasingly complex and varied. The term “tracery” itself can be traced back to the term “measured work“. It is a shape that can be geometrically constructed exclusively from circles, as our exhibit also shows. The tracery serves to subdivide the arch field (“couronnement“, see figure 4) situated above the “impost line” (the connecting line of the “imposts“, i.e. the load-bearing stones of an arch).

And now … the mathematics:

The geometry of the tracery is limited to the use of compasses and rulers. The individual constructions use the Pythagorean theorem (see also the exhibit “Proof without words: Pythagoras for laying” and) and the 2nd law of rays, as well as the Vieta root theorem for solving quadratic equations. Three of the basic constructions are shown below.

(I) Pointed arch with one incircle

In this construction, the inscribed circle with radius $r$ touches both arcs from the inside (each as parts of the arc of circles with radius $R\gt r$ ) and the base side of length $R$ (cf. Figure 4).

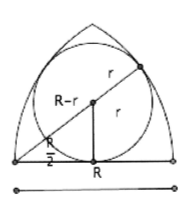
Following the Pythagorean theorem, we get (cf. Figure 4):

$r^2+\left(\frac{R}{2}\right)^2=(R-r)^2,$

i.e.

$r^2+R^2/4=R^2-2Rr+r^2.$

Thus $2Rr=\frac{3}{4}R^2$ or more precisely $r=\frac{3}{8}R$ . So the radius of the incircle relates to the radius of the arcs as $3:8$ .

(II) Pointed arch with a small circle above a semicircle

In this construction, the small circle with radius $r$ touches both arcs from the inside, which are parts of circles with radius $R\gt r$ , and a semicircle with radius $R/2$ from the outside (cf. Figure 5).

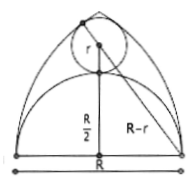
Following the Pythagorean theorem, we get:

$\left(\frac{R}{2}\right)^2+\left(r+\frac{R}{2}\right)^2=(R-r)^2,$

i.e.

$R^2/4+r^2+Rr+R^2/4=R^2-2Rr+r^2.$

From this follows: $3Rr=R^2/2$ and thus $r=R/6$ . The radii of the small circle and the semicircle below it therefore behave like $1:6$ .

(III) Pointed arch with circle over two semicircles

In this construction, a circle of radius $r$ from the inside touches both arcs, which are parts of circles of radius $R\gt r$ , and — lying below them — two semicircles of radius $R/2$ from the outside (cf. Figure 6).

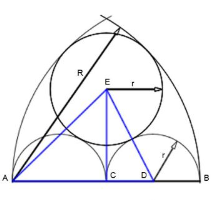
Following the Pythagorean theorem (in the triangle $CDE$ ), $R=\lvert\overline{AB}\rvert$ , $r'=\lvert\overline{CD}\rvert=R/4$ and $h=\lvert\overline{CE}\rvert$ on the one hand gives the equation

$\left(r+\frac{R}{4}\right)^2-\left(\frac{R}{4}\right)^2=h^2$

and on the other hand (in the triangle $ACE$ )

$(R-r)^2-\left(\frac{R}{2}\right)^2=h^2.$

That is

$r^2+Rr/2+R^2/16-R^2/16=R^2-2Rr+r^2-R^2/4.$

So $5Rr/2= 3R^2/4$ and therefore $r=\frac{3}{10} R$ , i.e. the radii of the “resting” circle and the circles whose parts form the arcs behave like $3:10$ .

Literature

[1] Binding, G.: Maßwerk, Darmstadt, 1989.

[2] Helten, L.: Mittelalterliches Maßwerk. Entstehung — Syntax — Topologie, Berlin, 2006.

[3] Schnellbächer, I.: Das Altenberger Westfenster, seine Botschaft im Licht der Bibel, Mariawald, 2009.

[4] http://www.janschuster.net/kirchenfenster/